
����Ŀ����ͼ����P( x�� y1)��Q (x�� y2)�ֱ�����������ͼ��C1��C2�ϵ���һ��. ��a �� x �� bʱ����-1 �� y1 - y2 �� 1���������������������a �� x �� b���ǡ����ں������������������a �� x �� b���ǡ������ں�������
���磬��P(x�� y1)��Q (x�� y2)�ֱ�����������y = 3x+1��y = 2x - 1ͼ���ϵ���һ�㣬��-3 �� x �� -1ʱ��y1 - y2 = (3x + 1) - (2x - 1) = x + 2��ͨ�����캯��y = x + 2�����о�����-3 �� x �� -1�ϵ����ʣ��õ��ú���ֵ�ķ�Χ��-1 �� y �� 1������-1 �� y1 - y2 �� 1���������������������-3 �� x �� -1���ǡ����ں�������
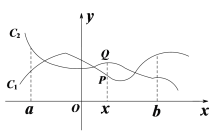
��1���жϺ���y = 3x + 2��y = 2x + 1��-2 �� x�� 0���Ƿ�Ϊ�����ں���������˵�����ɣ�
��2��������y = x2 - x��y = x - a��0 �� x �� 2���ǡ����ں���������a��ȡֵ��Χ��
���𰸡���1���ǣ����ɼ���������2��![]()
��������
��1��ͨ����������![]() ������һ�κ��������ʿɵó��ú�����0��x��2�ϵ����������ֱ����x=0��x=2���ɵó�y��ȡֵ��Χ���ɴ˼��ɵó����ۣ�
������һ�κ��������ʿɵó��ú�����0��x��2�ϵ����������ֱ����x=0��x=2���ɵó�y��ȡֵ��Χ���ɴ˼��ɵó����ۣ�
��2���ɺ���y=x2-x��y = x - a��0��x��2���ǡ����ں����������캯��![]() ��������������0 �� x �� 2������ȡֵ��Χ���������ֵ��1����Сֵ��-1�������a�IJ���ʽ�鼴�ɵó����ۣ�
��������������0 �� x �� 2������ȡֵ��Χ���������ֵ��1����Сֵ��-1�������a�IJ���ʽ�鼴�ɵó����ۣ�
�⣺��1���ǡ����ں�������
�������£�![]() �����캯��
�����캯��![]() ��
��
![]() ��
��![]() ������
������![]() �����������
�����������
![]() ��
��![]() ʱ�����������ֵ1����
ʱ�����������ֵ1����![]() ʱ����������Сֵ
ʱ����������Сֵ![]() ����
����![]() .
.
![]() ��
��
������![]() ��
��![]() ��
��![]() ���ǡ����ں�������
���ǡ����ں�������
��2��![]() �����캯��
�����캯��![]() ��
��
![]() ����������Ϊ
����������Ϊ![]()
��![]() ������
������![]() �Ŀ������ϣ�
�Ŀ������ϣ�
![]() ��
��![]() ʱ����������Сֵ
ʱ����������Сֵ![]() ��
��
��![]() ��
��![]() ʱ�����������ֵ
ʱ�����������ֵ![]() ����
����![]() ��
��
![]() ����
����![]() ��
��![]() ��
��![]() ���ǡ����ں�������
���ǡ����ں�������
![]() ����
����![]() ��
��
![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����3�֣���ͼ���ִ���B����ÿСʱ60������ٶ�����ƫ��20�㷽�����ٺ��У���B���۲����Aλ����ƫ��50�㷽���ϣ��ִ�����40���ӵ���C������C���۲����Aλ�ڱ�ƫ��10�㷽���ϣ���C�������A�ľ����ǣ� ��

A��20���� B��40���� C��![]() ���� D��
���� D��![]() ����
����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
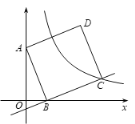
����Ŀ����ͼ����ֱ������ϵ�У�������ABCD�Ƶ�A��0��6����ת������B����x����ʱ����C�պ����ڷ���������![]() ��k��0��x��0)��ͼ���ϣ���֪sin��OAB��
��k��0��x��0)��ͼ���ϣ���֪sin��OAB��![]() .
.
��1�����������ı���ʽ��
��2������������![]() ��ͼ���Ƿ�AD�ߵ��е㣬��˵�����ɣ�
��ͼ���Ƿ�AD�ߵ��е㣬��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C����PΪ�߶�BC��һ�㣬����P��ֱ���ɡ�x���ڵ�F����������
��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C����PΪ�߶�BC��һ�㣬����P��ֱ���ɡ�x���ڵ�F����������![]() �ڵ�E��
�ڵ�E��
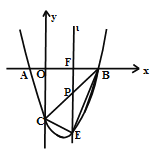
��1����A��B��C��������ꣻ
��2������P���߶�BC���˶�ʱ�����߶�PE�������ֵ��
��3����PEȡ���ֵʱ����������![]() ����ƽ�Ƶõ�������
����ƽ�Ƶõ�������![]() ��������
��������![]() ���߶�BE���ڵ�M����ֱ��CM����BCE�������Ϊ1��2�����֣���������
���߶�BE���ڵ�M����ֱ��CM����BCE�������Ϊ1��2�����֣���������![]() Ӧ����ƽ�Ƽ�����λ���ȿɵõ�������
Ӧ����ƽ�Ƽ�����λ���ȿɵõ�������![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
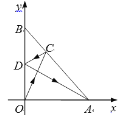
����Ŀ����ͼ��һ�����ߴӵ�O��������ھ���A��1��0����B��0��1���ľ����ϵĵ�C����AB��������յ�������y��λ�õľ����ϵ�D�㣬���y���ٷ���Ĺ���ǡ�þ�����A�����C������Ϊ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�ӿ����ǻ�У�����裬ij����Ϊ�Ե�ѧУ�ɹ�һ�� ![]() ��
��![]() �����ͺŵ�һ����������г����鷢�֣�����ÿ��
�����ͺŵ�һ����������г����鷢�֣�����ÿ�� ![]() ��һ����ļ۸��ÿ��
��һ����ļ۸��ÿ�� ![]() ��һ����ļ۸��
��һ����ļ۸�� ![]() ��Ԫ������
��Ԫ������![]() ��Ԫǡ���ܹ���
��Ԫǡ���ܹ��� ![]() ��
�� ![]() ��һ�����
��һ����� ![]() ��
�� ![]() ��һ�����
��һ�����
��1�������ÿ�� ![]() �͡�
�͡�![]() ��һ����ļ۸���Ƕ�����Ԫ��
��һ����ļ۸���Ƕ�����Ԫ��
��2����������ƻ��ɹ� ![]() �͡�
�͡�![]() ��һ�����
��һ����� ![]() �ף���Ͷ���ʽ�
�ף���Ͷ���ʽ� ![]() ��Ԫ. ����������أ�Ԥ������ÿ��
��Ԫ. ����������أ�Ԥ������ÿ�� ![]() ��һ����ļ۸䣬ÿ��
��һ����ļ۸䣬ÿ�� ![]() ��һ����ļ۸�Ƚ�������
��һ����ļ۸�Ƚ������� ![]() �� ��������깺��
�� ��������깺�� ![]() ��һ���
��һ��� ![]() ��.
��.
����д������������Ͷ���ʽ� ![]() ����Ԫ���빺��
����Ԫ���빺�� ![]() ��һ���
��һ��� ![]() ���ף�֮��ĺ�����ϵʽ ��
���ף�֮��ĺ�����ϵʽ ��
�����������깺�� ![]() ��һ������ܷ��ò����ڹ���
��һ������ܷ��ò����ڹ��� ![]() ��һ������ܷ��ã���ô��������������ҪͶ�������Ԫ������ɲɹ��ƻ���
��һ������ܷ��ã���ô��������������ҪͶ�������Ԫ������ɲɹ��ƻ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����������ͷ�����������ͼ������![]() ����
����![]() Ϊ˫�����ϵ�һ�㣬
Ϊ˫�����ϵ�һ�㣬![]() Ϊ����ƽ����һ���㣬
Ϊ����ƽ����һ���㣬![]() ��ֱ��
��ֱ��![]() �ᣬ
�ᣬ![]() ��ֱ��
��ֱ��![]() �ᣬ����ֱ���
�ᣬ����ֱ���![]() ��
��![]() .
.
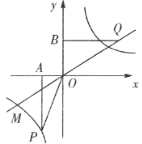
��1��д�������������ͷ����������Ĺ�ϵʽ.
��2������![]() ��ֱ��
��ֱ��![]() ���˶�ʱ��ֱ��
���˶�ʱ��ֱ��![]() ���Ƿ���������ĵ�
���Ƿ���������ĵ�![]() ��ʹ��
��ʹ��![]() ��
��![]() �������ȣ�������ڣ������������ꣻ��������ڣ���˵������.
�������ȣ�������ڣ������������ꣻ��������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵxOy�У����������������A��B��C���������¶��壺�����ε��κ�һ���߾���ij��������ƽ�У���A��B��C���㶼�ھ��ε��ڲ���߽��ϣ���Ƹþ���Ϊ��A��B��C�ġ�������Ρ����ڵ�A��B��C�����С�������Ρ��У������������С�ľ��Σ���Ƹþ���Ϊ��A��B��C�ġ����������Ρ���
��ͼ1������DEFG������IJCH���ǵ�A��B��C�ġ�������Ρ�������IJCH�ǵ�A��B��C�ġ����������Ρ���
��ͼ2����֪M��4��1����N����2��3������P��m��n����
��1������m��1��n��4�����M��N��P�ġ����������Ρ����ܳ�Ϊ�� �������Ϊ�� ����
����m��1����M��N��P�ġ����������Ρ������Ϊ24����n��ֵ��
��2������P��ֱ��y����2x+4�ϣ�
�����M��N��P�ġ����������Ρ��������Сֵ����ʱm��ȡֵ��Χ��
������M��N��P�ġ����������Ρ�Ϊ������ʱ�����P�����ꣻ
��3������P��m��n����������y��ax2+bx+c�ϣ��ҵ���M��N��P�ġ����������Ρ����Ϊ12ʱ����2��m�ܩ�1��1��m��3��ֱ��д�������ߵĽ���ʽ��
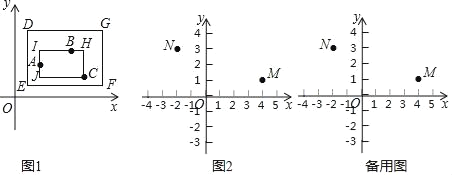
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC����A=30����ֱ��a��b������C��ֱ��b�ϣ�ֱ��a��AB�ڵ�D����AC�ڵ�E������1=145��������2�Ķ�����( )

A.30��B.35��C.40��D.45��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com