
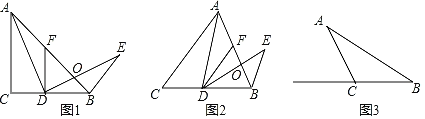
【题目】在△ABC中,AC=BC,∠ACB=α,点D为直线BC上一动点,过点D作DF∥AC交直线AB于点F,将AD绕点D顺时针旋转α得到ED,ED交直线AB于点O,连接BE.
(1)问题发现:
如图1,α=90°,点D在边BC上,猜想:
①AF与BE的数量关系是 ;
②∠ABE= 度.
(2)拓展探究:
如图2,0°<α<90°,点D在边BC上,请判断AF与BE的数量关系及∠ABE的度数,并给予证明.
(3)解决问题
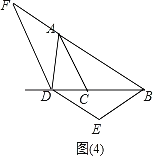
如图3,90°<α<180°,点D在射线BC上,且BD=3CD,若AB=8,请直接写出BE的长.
【答案】(1)①AF=BE,②90°;(2)AF=BE,∠ABE=α.理由见解析;(3)BE的长为2或4.
【解析】
(1)①由等腰直角三角形的判定和性质可得:∠ABC=45°,由平行线的性质可得∠FDB=∠C=90°,进而可得由等角对等边可得DF=DB,由旋转可得:∠ADF=∠EDB,DA=DE,继而可知△ADF≌△EDB,继而即可知AF=BE;
②由全等三角形的性质可知∠DAF=∠E,继而由三角形内角和定理即可求解;
(2)由平行线的性质可得∠ACB=∠FDB=α,∠CAB=∠DFB,由等边对等角可得∠ABC=∠CAB,进而根据等角对等边可得DB=DF,再根据全等三角形的判定方法证得△ADF≌△EDB,进而可得求证AF=BE,∠ABE=∠FDB=α;
(3)分两种情况考虑:①如图(3)中,当点D在BC上时,②如图(4)中,当点D在BC的延长线上时,由平行线分线段成比例定理可得![]() 、
、![]() ,代入数据求解即可;
,代入数据求解即可;
(1)问题发现:
如图1中,设AB交DE于O.
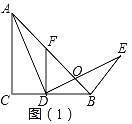
∵∠ACB=90°,AC=BC,
∴∠ABC=45°,
∵DF∥AC,
∴∠FDB=∠C=90°,
∴∠DFB=∠DBF=45°,
∴DF=DB,
∵∠ADE=∠FDB=90°,
∴∠ADF=∠EDB,
∵DA=DE,DF=DB
∴△ADF≌△EDB(SAS),
∴AF=BE,∠DAF=∠E,
∵∠AOD=∠EOB,
∴∠ABE=∠ADO=90°
故答案为:①AF=BE,②90°.
(2)拓展探究:
结论:AF=BE,∠ABE=α.理由如下:
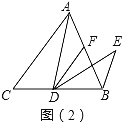
∵DF‖AC
∴∠ACB=∠FDB=α,∠CAB=∠DFB,
∵AC=BC,
∴∠ABC=∠CAB,
∴∠ABC=∠DFB,
∴DB=DF,
∵∠ADF=∠ADE﹣∠FDE,∠EDB=∠FDB﹣∠FDE,
∴∠ADF=∠EDB,
∵AD=DE,DB=DF
∴△ADF≌△EDB(SAS),
∴AF=BE,∠AFD=∠EBD
∵∠AFD=∠ABC+∠FDB,∠DBE=∠ABD+∠ABE,
∴∠ABE=∠FDB=α.
(3)解决问题
①如图(3)中,当点D在BC上时,
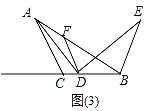
由(2)可知:BE=AF,
∵DF∥AC,
∴![]() ,
,
∵AB=8,
∴AF=2,
∴BE=AF=2,
②如图(4)中,当点D在BC的延长线上时,
∵AC∥DF,
∴![]() ,
,
∵AB=8,
∴BE=AF=4,
故BE的长为2或4.


科目:初中数学 来源: 题型:
【题目】2019年9月30日,由著名导演李仁港执导的电影《攀登者》在各大影院上映后,好评不断,小亮和小丽都想去观看这部电影,但是只有一张电影票,于是他们决定采用模球的办法决定胜负,获胜者去看电影,游戏规则如下:在一个不透明的袋子中装有编号1-4的四个球(除编号外都相同),从中随机摸出一个球,记下数字后放回,再从中摸出一个球,记下数字,若两次数字之和大于5,则小亮获胜,若两次数字之和小于5,则小丽获胜.
(1)请用列表或画树状图的方法表示出随机摸球所有可能的结果;
(2)分别求出小亮和小丽获胜的概率,并判断这种游戏规则对两人公平吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是某公园一圆形喷水池,在池中心竖直安装一根水管OA=1.25m,A处是喷头,水流在各个方向沿形状相同的抛物线落下,水落地后形成一个圆,圆心为O,直径为线段CB.建立如图所示的平面直角坐标系,若水流路线达到最高处时,到x轴的距离为2.25m,到y轴的距离为1m,则水落地后形成的圆的直径CB=_____m.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行汉字听写大赛,学习对参赛者获奖情况进行统计,根据比赛成绩列出统计表,并绘制了扇形统计图
(1)参加此次比赛的学生共______________人.
(2)![]()
(3)若从一等奖中随机抽取两名学生,参加市级汉字听写大赛,请用树状图或列表的方法,求出所选的两名学生正好为一男一女的概率.
等次 | 男生 | 女生 |
一等奖 | 3 | m |
二等奖 | 6 | 12 |
三等奖 | 8 | 9 |
鼓励奖 | 6 | n |

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算:①![]() ;②(x﹣2y)2=x2﹣4y2;③(﹣a)4a3=﹣a7;④x10÷x5=x2,其中错误的个数是( )
;②(x﹣2y)2=x2﹣4y2;③(﹣a)4a3=﹣a7;④x10÷x5=x2,其中错误的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解九年级男同学1000米跑步的成绩,随机抽取了部分男生进行测试,并将测试成绩分为A、B、C、D四个等级,绘制了不完整的成绩等级频数表和扇形统计图.
成绩等级 | 频数 |
A | 24 |
B | 10 |
C | b |
D | 2 |
合计 | a |
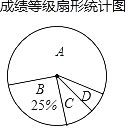
(1)表中a= ,b= ;
(2)扇形图中C的圆心角度数是 ;
(3)若该校共有九年级男生600人,请估计没有获得A等级的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
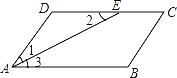
【题目】如图,在ABCD中,AE平分∠BAD交DC于点E,AD=5cm,AB=8cm.
(1)求EC的长.
(2)作∠BCD的平分线交AB于F,求证:四边形AECF为平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=a(x+1)(x﹣m)(a为非零常数,1<m<2),当x<﹣1时,y随x的增大而增大,说法正确的是( )
A.若图象经过点(0,1),则﹣![]() <a<0
<a<0
B.若x>﹣![]() 时,则y随x的增大而增大
时,则y随x的增大而增大
C.若(﹣2020,y1),(2020,y2)是函数图象上的两点,则y1<y2
D.若图象上两点(![]() ,y1),(
,y1),(![]() +n,y2)对一切正数n,总有y1>y2,则
+n,y2)对一切正数n,总有y1>y2,则![]() ≤m<2
≤m<2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,点E是A边上一点,且AE=![]() ,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为_____.
,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com