
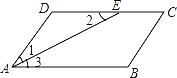
【题目】如图,在ABCD中,AE平分∠BAD交DC于点E,AD=5cm,AB=8cm.
(1)求EC的长.
(2)作∠BCD的平分线交AB于F,求证:四边形AECF为平行四边形.
【答案】(1)3 cm;(2)见解析
【解析】
(1)首先根据角平分线的性质可得∠1=∠3,再根据平行线的性质可得∠3=∠2,利用等量代换可得∠1=∠2,根据等角对等边可得AD=DE,再根据线段的和差关系可得EC长;
(2)首先根据平行四边形的性质可得∠DAB=∠DCB,CD∥AB,再根据角平分线的性质可得∠3=∠ECF,再证明AE∥CF,根据两组对边分别平行的四边形是平行四边形可证明四边形AECF为平行四边形.
解:(1)如图,
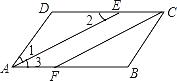
∵AE平分∠BAD,
∴∠1=∠3,
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠3=∠2,
∴∠1=∠2,
∴AD=DE=5cm,
∵AB=8cm,
∴EC=8﹣5=3cm;
(2)∵四边形ABCD是平行四边形,
∴∠DAB=∠DCB,CD∥AB,
∵AE平分∠BAD,
∴∠3=![]() ,
,
∵CF平分∠DCB,
∴∠ECF=![]() ,
,
∴∠3=∠ECF,
∵∠2=∠3,
∴∠2=∠ECF,
∴AE∥CF,
∴四边形AECF为平行四边形.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
【题目】一辆汽车在某次行驶过程中,油箱中的剩余油量y(升)与行驶路程x(千米)之间是一次函数关系,其部分图象如图所示.
(1)求y关于x的函数关系式;(不需要写定义域)
(2)已知当油箱中的剩余油量为8升时,该汽车会开始提示加油,在此次行驶过程中,行驶了500千米时,司机发现离前方最近的加油站有30千米的路程,在开往该加油站的途中,汽车开始提示加油,这时离加油站的路程是多少千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+2bx+1﹣2b(b为常数).
(1)若点(2,5)在该抛物线上,求b的值;
(2)若该抛物线的顶点坐标是(m,n),求n关于m的函数解析式;
(3)若抛物线与x轴交点之间的距离大于4,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AC=BC,∠ACB=α,点D为直线BC上一动点,过点D作DF∥AC交直线AB于点F,将AD绕点D顺时针旋转α得到ED,ED交直线AB于点O,连接BE.
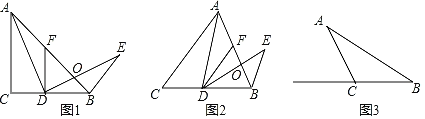
(1)问题发现:
如图1,α=90°,点D在边BC上,猜想:
①AF与BE的数量关系是 ;
②∠ABE= 度.
(2)拓展探究:
如图2,0°<α<90°,点D在边BC上,请判断AF与BE的数量关系及∠ABE的度数,并给予证明.
(3)解决问题
如图3,90°<α<180°,点D在射线BC上,且BD=3CD,若AB=8,请直接写出BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是矩形,等腰△ODE中,OE=DE,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点B、E在反比例函数y=![]() 的图象上,OA=5,OC=1,则△ODE的面积为( )
的图象上,OA=5,OC=1,则△ODE的面积为( )
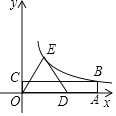
A.2.5B.5C.7.5D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
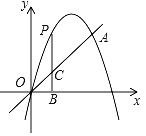
【题目】已知:如图,抛物线y=ax2+4x+c经过原点O(0,0)和点A (3,3),P为抛物线上的一个动点,过点P作x轴的垂线,垂足为B(m,0),并与直线OA交于点C.
(1)求抛物线的解析式;
(2)当点P在直线OA上方时,求线段PC的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx+6与二次函数y=ax2+c的图象的一个交点坐标为(1,2),另一个交点是该二次函数图象的顶点.
(1)求k,a,c的值;
(2)过点A(0,m)(0<m<6)且垂直于y轴的直线与二次函数y=ax2+c的图象相交于B,C两点,点O为坐标原点,记W=OA2+BC2,求W关于m的函数解析式,并求W的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
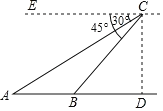
【题目】如图,在直升机的镜头下,观测东营市清风湖A处的俯角为30°,B处的俯角为45°,如果此时直升机镜头C处的高度CD为300米,点A、B、D在同一条直线上,则A、B两点间的距离为____米.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
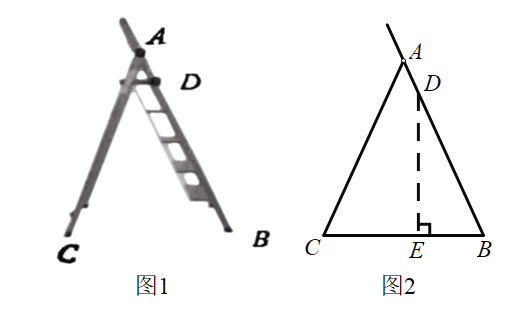
【题目】人字折叠梯完全打开后如图1所示,B,C是折叠梯的两个着地点,D是折叠梯最高级踏板的固定点.图2是它的示意图,AB=AC,BD=140cm,∠BAC=40°,求点D离地面的高度DE.(结果精确到0.1cm;参考数据sin70°≈0. 94,cos70°≈0.34,sin20°≈0.34,cos20°≈0.94)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com