
【题目】已知:如图,抛物线y=ax2+4x+c经过原点O(0,0)和点A (3,3),P为抛物线上的一个动点,过点P作x轴的垂线,垂足为B(m,0),并与直线OA交于点C.
(1)求抛物线的解析式;
(2)当点P在直线OA上方时,求线段PC的最大值.
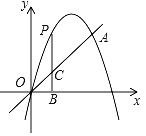
【答案】(1)y=﹣x2+4x;(2)![]() .
.
【解析】
(1)把A与O坐标代入抛物线解析式求出a与c的值,即可求出解析式;
(2)根据题意表示出P与C的纵坐标,进而表示出线段PC的长,确定出最大值即可.
解:(1)把O(0,0),A(3,3)代入得:![]() ,
,
解得:![]() ,
,
则抛物线解析式为y=﹣x2+4x;
(2)设直线OA解析式为y=kx,
把A(3,3)代入得:k=1,即直线OA解析式为y=x,
∵PB⊥x轴,
∴P,C,B三点横坐标相等,
∵B(m,0),
∴把x=m代入y=x中得:y=m,即C(m,m),
把x=m代入y=﹣x2+4x中得:y=﹣m2+4m,即P(m,﹣m2+4m),
∵P在直线OA上方,
∴PC=﹣m2+4m﹣m=﹣m2+3m(0<m<3),
当m= 时,PC取得最大值,最大值为
时,PC取得最大值,最大值为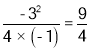 .
.


科目:初中数学 来源: 题型:
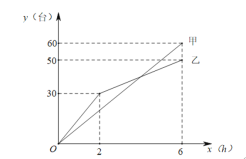
【题目】甲、乙两个电子团队维护一批电脑,维护电脑的台数y(台)与维护需要的工作时间x(h)(0≤x≤6)之间关系如图所示,请依据图象提供的信息解答下列问题:
(1)求乙队维护电脑的台数y(台)关于维护的时间x(h)的关系式;
(2)当x为多少时,甲、乙两队维护的电脑台数一样.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行汉字听写大赛,学习对参赛者获奖情况进行统计,根据比赛成绩列出统计表,并绘制了扇形统计图
(1)参加此次比赛的学生共______________人.
(2)![]()
(3)若从一等奖中随机抽取两名学生,参加市级汉字听写大赛,请用树状图或列表的方法,求出所选的两名学生正好为一男一女的概率.
等次 | 男生 | 女生 |
一等奖 | 3 | m |
二等奖 | 6 | 12 |
三等奖 | 8 | 9 |
鼓励奖 | 6 | n |

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解九年级男同学1000米跑步的成绩,随机抽取了部分男生进行测试,并将测试成绩分为A、B、C、D四个等级,绘制了不完整的成绩等级频数表和扇形统计图.
成绩等级 | 频数 |
A | 24 |
B | 10 |
C | b |
D | 2 |
合计 | a |
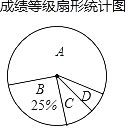
(1)表中a= ,b= ;
(2)扇形图中C的圆心角度数是 ;
(3)若该校共有九年级男生600人,请估计没有获得A等级的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
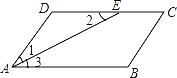
【题目】如图,在ABCD中,AE平分∠BAD交DC于点E,AD=5cm,AB=8cm.
(1)求EC的长.
(2)作∠BCD的平分线交AB于F,求证:四边形AECF为平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数a,b,定义新运算“*”:a*b=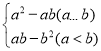 ,例如:4*2,因为4>2,所以4*2=42﹣4×2=8.
,例如:4*2,因为4>2,所以4*2=42﹣4×2=8.
(1)求(﹣7)*(﹣2)的值;
(2)若x1,x2是一元次方程x2﹣5x﹣6=0的两个根,求x1*x2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=a(x+1)(x﹣m)(a为非零常数,1<m<2),当x<﹣1时,y随x的增大而增大,说法正确的是( )
A.若图象经过点(0,1),则﹣![]() <a<0
<a<0
B.若x>﹣![]() 时,则y随x的增大而增大
时,则y随x的增大而增大
C.若(﹣2020,y1),(2020,y2)是函数图象上的两点,则y1<y2
D.若图象上两点(![]() ,y1),(
,y1),(![]() +n,y2)对一切正数n,总有y1>y2,则
+n,y2)对一切正数n,总有y1>y2,则![]() ≤m<2
≤m<2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(11,0),点B(0,6),点P为BC边上的动点(点P不与点B、C重合),经过点O、P折叠该纸片,得点B′和折痕OP.设BP=t.
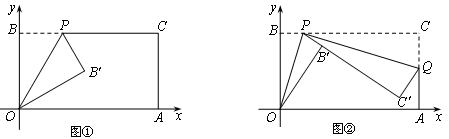
(Ⅰ)如图①,当∠BOP=300时,求点P的坐标;
(Ⅱ)如图②,经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ,若AQ=m,试用含有t的式子表示m;
(Ⅲ)在(Ⅱ)的条件下,当点C′恰好落在边OA上时,求点P的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用各种盛水容器可以制作精致的家用流水景观(如图1).
科学原理:如图2,始终盛满水的圆体水桶水面离地面的高度为H(单位:m),如果在离水面竖直距离为h(单校:cm)的地方开大小合适的小孔,那么从小孔射出水的射程(水流落地点离小孔的水平距离)s(单位:cm)与h的关系为s2=4h(H—h).
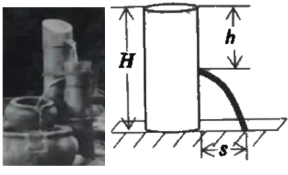
应用思考:现用高度为20cm的圆柱体望料水瓶做相关研究,水瓶直立地面,通过连注水保证它始终盛满水,在离水面竖直距高h cm处开一个小孔.
(1)写出s2与h的关系式;并求出当h为何值时,射程s有最大值,最大射程是多少?
(2)在侧面开两个小孔,这两个小孔离水面的竖直距离分别为a,b,要使两孔射出水的射程相同,求a,b之间的关系式;
(3)如果想通过垫高塑料水瓶,使射出水的最大射程增加16cm,求整高的高度及小孔离水面的竖直距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com