
【题目】已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(11,0),点B(0,6),点P为BC边上的动点(点P不与点B、C重合),经过点O、P折叠该纸片,得点B′和折痕OP.设BP=t.
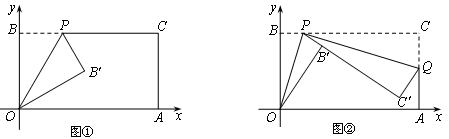
(Ⅰ)如图①,当∠BOP=300时,求点P的坐标;
(Ⅱ)如图②,经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ,若AQ=m,试用含有t的式子表示m;
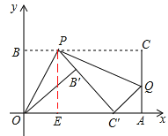
(Ⅲ)在(Ⅱ)的条件下,当点C′恰好落在边OA上时,求点P的坐标(直接写出结果即可).
【答案】(Ⅰ)根据题意,∠OBP=90°,OB=6。
在Rt△OBP中,由∠BOP=30°,BP=t,得OP=2t。
∵OP2=OB2+BP2,即(2t)2=62+t2,解得:t1=![]() ,t2=-
,t2=-![]() (舍去).
(舍去).
∴点P的坐标为(![]() ,6)。
,6)。
(Ⅱ)∵△OB′P、△QC′P分别是由△OBP、△QCP折叠得到的,
∴△OB′P≌△OBP,△QC′P≌△QCP。
∴∠OPB′=∠OPB,∠QPC′=∠QPC。
∵∠OPB′+∠OPB+∠QPC′+∠QPC=180°,∴∠OPB+∠QPC=90°。
∵∠BOP+∠OPB=90°,∴∠BOP=∠CPQ。
又∵∠OBP=∠C=90°,∴△OBP∽△PCQ。∴![]() 。
。
由题意设BP=t,AQ=m,BC=11,AC=6,则PC=11-t,CQ=6-m.
∴![]() 。∴
。∴![]() (0<t<11)。
(0<t<11)。
(Ⅲ)点P的坐标为(![]() ,6)或(
,6)或(![]() ,6)。
,6)。
【解析】(Ⅰ)根据题意得,∠OBP=90°,OB=6,在Rt△OBP中,由∠BOP=30°,BP=t,得OP=2t,然后利用勾股定理,即可得方程,解此方程即可求得答案。
(Ⅱ)由△OB′P、△QC′P分别是由△OBP、△QCP折叠得到的,可知△OB′P≌△OBP,
△QC′P≌△QCP,易证得△OBP∽△PCQ,然后由相似三角形的对应边成比例,即可求得答案。
(Ⅲ)首先过点P作PE⊥OA于E,易证得△PC′E∽△C′QA,由勾股定理可求得C′Q的长,然后利用相似三角形的对应边成比例与![]() ,即可求得t的值:
,即可求得t的值:
过点P作PE⊥OA于E,∴∠PEA=∠QAC′=90°。
∴∠PC′E+∠EPC′=90°。
∵∠PC′E+∠QC′A=90°,∴∠EPC′=∠QC′A。
∴△PC′E∽△C′QA。∴![]() 。
。
∵PC′=PC=11-t,PE=OB=6,AQ=m,C′Q=CQ=6-m,
∴![]() 。
。
∴![]() 。
。
∵![]() ,即
,即![]() ,∴
,∴![]() ,即
,即![]() 。
。
将![]() 代入,并化简,得
代入,并化简,得![]() 。解得:
。解得:![]() 。
。
∴点P的坐标为(![]() ,6)或(
,6)或(![]() ,6)。
,6)。


科目:初中数学 来源: 题型:
【题目】如图,△ABD≌△CDB,且AB,CD是对应边.下面四个结论中不正确的是( )

A. △ABD和△CDB的面积相等B. △ABD和△CDB的周长相等
C. ∠A+∠ABD=∠C+∠CBDD. AD∥BC,且AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )

A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
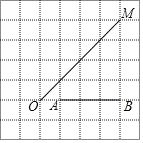
【题目】如图,在每个小正方形的边长为1的网格中,点O,A,B,M均在格点上,P为线段OM上的一个动点.
(1)OM的长等于_______;
(2)当点P在线段OM上运动,且使PA2+PB2取得最小值时,请借助网格和无刻度的直尺,在给定的网格中画出点P的位置,并简要说明你是怎么画的.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知OA,OB是⊙O的半径,且OA⊥OB,垂足为O,P是射线OA上的一点(点A除外),直线BP交⊙O于点Q,过Q作⊙O的切线交射线OA于点E.
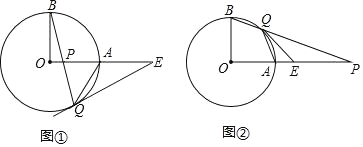
(1)如图①,点P在线段OA上,若∠OBQ=15°,求∠AQE的大小;
(2)如图②,点P在OA的延长线上,若∠OBQ=65°,求∠AQE的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为![]() ,为保护廊桥的安全,在该抛物线上距水面
,为保护廊桥的安全,在该抛物线上距水面![]() 高为8米的点
高为8米的点![]() 、
、![]() 处要安装两盏警示灯,则这两盏灯的水平距离
处要安装两盏警示灯,则这两盏灯的水平距离![]() 是____米.
是____米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED,其中一定成立的____(把你认为正确结论的序号都填上)
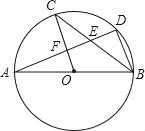
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高校学生会在某天午餐后,随机调查了部分同学就餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
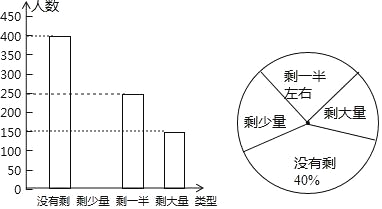
(1)这次被调查的同学共有名;
(2)补全条形统计图;
(3)计算在扇形统计图中剩大量饭菜所对应扇形圆心角的度数;
(4)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐.据此估算,该校20000名学生一餐浪费的食物可供多少人食用一餐?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com