
【题目】如图,已知![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求证:![]() ;
;
(2)求证:![]() .
.
【答案】(1)见解析;(2)见解析
【解析】
(1)根据垂直的定义和等式的基本性质可得∠EAC=∠BAF,然后利用SAS即可证出![]() ;
;
(2)设AB与EC的交点为O,根据全等三角形的性质可得∠AEC=∠ABF,然后根据对顶角相等可得∠AOE=∠BOM,再根据三角形的内角和定理和等量代换即可求出∠OMB=90°,最后根据垂直的定义即可证明.
解:(1)∵![]() ,
,![]() ,
,
∴∠EAB=∠CAF=90°
∴∠EAB+∠BAC=∠CAF+∠BAC
∴∠EAC=∠BAF
在△AEC和△ABF中
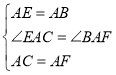
∴![]() (SAS)
(SAS)
(2)设AB与EC的交点为O,如下图所示
∵![]()
∴∠AEC=∠ABF
∵∠AOE=∠BOM
∴∠OMB=180°-∠ABF-∠BOM=180°-∠AEC-∠AOE=∠EAB=90°
∴![]()


科目:初中数学 来源: 题型:
【题目】从宁海县到某市,可乘坐普通列车或高铁,已知高铁的行驶路程与普通列车的行驶路程之和是920千米,而普通列车的行驶路程是高铁的行驶路程的1.3倍.
(1)求普通列车的行驶路程;
(2)若高铁的平均速度(千米/时)是普通列车的平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求高铁的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
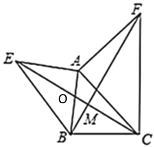
【题目】已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(11,0),点B(0,6),点P为BC边上的动点(点P不与点B、C重合),经过点O、P折叠该纸片,得点B′和折痕OP.设BP=t.
(Ⅰ)如图①,当∠BOP=300时,求点P的坐标;
(Ⅱ)如图②,经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ,若AQ=m,试用含有t的式子表示m;
(Ⅲ)在(Ⅱ)的条件下,当点C′恰好落在边OA上时,求点P的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
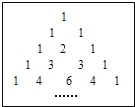
【题目】我国宋朝数学家杨辉在他的著作《详解九章算法》中提出如图,此表揭示了(a+b)n(n为非负整数)展开式的各项系数的规律,例如:(a+b)0=1,它只有一项,系数为1;(a+b)1=a+b,它有两项,系数分别为1,1;(a+b)2=a2+2ab+b2,它有三项,系数分别为1,2,1;(a+b)3=a3+3a2b+3ab2+b3,它有四项,系数分别为1,3,3,1;…;根据以上规律,(a+b)5展开式共有六项,系数分别为______,拓展应用:(a﹣b)4=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形ABCD中,E是AB边的中点,DE交AC于点F,AC、DE把它分成的四部分的面积分别为S1S2S3S4,下面结论:
①只有一对相似三角形
②EF:ED=1:2
③S1:S2:S3:S4=1:2:4:5
其中正确的结论是( )
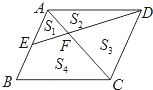
A.①③ B.③ C.① D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN周长取最小值时,则∠MPN的度数为( )

A. 140° B. 100° C. 50° D. 40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市出租车计费办法如图所示.根据图象信息,下列说法错误的是( )
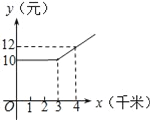
A. 出租车起步价是10元
B. 在3千米内只收起步价
C. 超过3千米部分(x>3)每千米收3元
D. 超过3千米时(x>3)所需费用y与x之间的函数关系式是y=2x+4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com