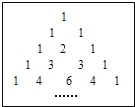
【题目】我国宋朝数学家杨辉在他的著作《详解九章算法》中提出如图，此表揭示了（a+b）n（n为非负整数）展开式的各项系数的规律，例如：（a+b）0＝1，它只有一项，系数为1；（a+b）1＝a+b，它有两项，系数分别为1，1；（a+b）2＝a2+2ab+b2，它有三项，系数分别为1，2，1；（a+b）3＝a3+3a2b+3ab2+b3，它有四项，系数分别为1，3，3，1；…；根据以上规律，（a+b）5展开式共有六项，系数分别为______，拓展应用：（a﹣b）4＝_______．
科目：初中数学 来源： 题型：
【题目】已知OA，OB是⊙O的半径，且OA⊥OB，垂足为O，P是射线OA上的一点（点A除外），直线BP交⊙O于点Q，过Q作⊙O的切线交射线OA于点E．
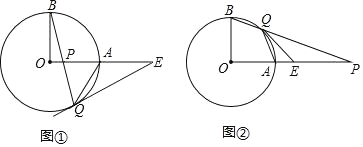
（1）如图①，点P在线段OA上，若∠OBQ=15°，求∠AQE的大小；
（2）如图②，点P在OA的延长线上，若∠OBQ=65°，求∠AQE的大小．
查看答案和解析>>
科目：初中数学 来源： 题型：
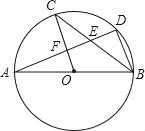
【题目】如图，AB是⊙O的直径，C，D是⊙O上的点，且OC∥BD，AD分别与BC，OC相交于点E，F，则下列结论：①AD⊥BD；②∠AOC=∠AEC；③CB平分∠ABD；④AF=DF；⑤BD=2OF；⑥△CEF≌△BED，其中一定成立的____（把你认为正确结论的序号都填上）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）探究新知：如图1，已知△ABC与△ABD的面积相等，试判断AB与CD的位置关系，并说明理由．
（2）结论应用：① 如图2，点M，N在反比例函数
（k＞0）的图象上，过点M作ME⊥y轴，过点N作NF⊥x轴，垂足分别为E，F．试证明：MN∥EF．
② 若①中的其他条件不变，只改变点M，N的位置如图3所示，请判断 MN与EF是否平行？请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某甜品店用
，
两种原料制作成甲、乙两款甜品进行销售，制作每份甜品的原料所需用量如下表所示.该店制作甲款甜品
份，乙款甜品
份，共用去原料2000克．
原料 款式 |
（克） |
（克） |
甲款甜品 | 30 | 15 |
乙款甜品 | 10 | 20 |
（1）求关于的函数表达式；
（2）已知每份甲甜品的利润为5元，每份乙甜品的利润为2元.假设两款甜品均能全部卖出.若获得总利润不少于360元，则至少要用去原料多少克？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某中学决定在“五·四艺术周”为一个节目制作A、B两种道具，共80个． 制作的道具需要甲、乙两种材料组合而成，现有甲种材料700件，乙种材料500件，已知组装A、B两种道具所需的甲、乙两种材料，如下表所示：
甲种材料（件） | 乙种材料（件） | |
A道具 | 6 | 8 |
B道具 | 10 | 4 |
经过计算，制作一个A道具的费用为5元，一个B道具的费用为4.5元． 设组装A种道具x个，所需总费用为y元．
（1）求y与x的函数关系式，并求出x的取值范围；
（2）问组装A种道具多少个时，所需总费用最少，最少费用是多少？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
