
【题目】(1)探究新知:如图1,已知△ABC与△ABD的面积相等,试判断AB与CD的位置关系,并说明理由.

(2)结论应用:① 如图2,点M,N在反比例函数![]() (k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.试证明:MN∥EF.
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.试证明:MN∥EF.
② 若①中的其他条件不变,只改变点M,N的位置如图3所示,请判断 MN与EF是否平行?请说明理由.
【答案】(1)AB∥CD.理由见解析;(2)证明见解析(3)MN∥EF.理由见解析.
【解析】
试题分析:(1)分别过点C,D,作CG⊥AB,DH⊥AB,然后证明四边形CGHD为平行四边形后可得AB∥CD;(2)①连结MF,NE. 设点M的坐标为(x1,y1),点N的坐标为(x2,y2).利用反比例函数的性质结合条件得出S△EFM =S△EFN.可得MN∥EF.(3)MN∥EF. 证明与①类似.
试题解析:(1)分别过点C,D,作CG⊥AB,DH⊥AB,垂足为G,H,
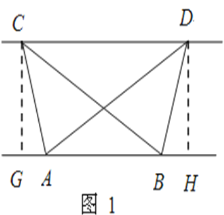
则∠CGA=∠DHB=90°.
∴ CG∥DH.
∵ △ABC与△ABD的面积相等,
∴ CG=DH.
∴ 四边形CGHD为平行四边形.
∴ AB∥CD.
(2)①连结MF,NE.
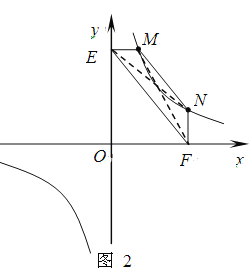
设点M的坐标为(x1,y1),点N的坐标为(x2,y2).
∵ 点M,N在反比例函数![]() (k>0)的图象上,
(k>0)的图象上,
∴ ![]() ,
,![]()
∵ ME⊥y轴,NF⊥x轴
∴ OE=y1,OF=x2.
∴ S△EFM=![]()
S△EFN=![]() .
.
∴S△EFM =S△EFN.
由(1)中的结论可知:MN∥EF.
② MN∥EF. 证明与①类似,略.

(若学生使用其他方法,只要解法正确,皆给分.)


科目:初中数学 来源: 题型:
【题目】《田亩比类乘除捷法》是我国古代数学家杨辉的著作,其中有一个数学问题:“直田积八百六十四步,只云长阔共六十步,问长多阔几何”.意思是:一块矩形田地的面积为864平方步,只知道它的长与宽共60步,问它的长比宽多多少步?根据题意得,长比宽多______步.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师把第一小组五名同学的成绩简记为:+10 ,-5 ,0 ,+8 ,-3 ,又知道记为0分的成绩表示90分,正数表示超过90分,则五名同学的平均成绩为多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在中考体育达标跳绳项目测试中,1分钟跳160次为达标,小敏记录了他预测时1分钟跳的次数分别为145,155,140,162,164,则他在该次预测中达标的概率是___。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B两座城市相距100千米,现计划在两城市间修筑一条高速公路(即线段AB).经测量,森林保护区中心P点既在A城市的北偏东30°的方向上,又在B城市的南偏东45°的方向上.已知森林保护区的范围是以P为圆心,35千米为半径的圆形区域内.请问:计划修筑的这条高速公路会不会穿越森林保护区?请通过计算说明.(参考数据:![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com