
【题目】某甜品店用![]() ,
,![]() 两种原料制作成甲、乙两款甜品进行销售,制作每份甜品的原料所需用量如下表所示.该店制作甲款甜品
两种原料制作成甲、乙两款甜品进行销售,制作每份甜品的原料所需用量如下表所示.该店制作甲款甜品![]() 份,乙款甜品
份,乙款甜品![]() 份,共用去
份,共用去![]() 原料2000克.
原料2000克.
原料 款式 |
(克) |
(克) |
甲款甜品 | 30 | 15 |
乙款甜品 | 10 | 20 |
(1)求![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)已知每份甲甜品的利润为5元,每份乙甜品的利润为2元.假设两款甜品均能全部卖出.若获得总利润不少于360元,则至少要用去![]() 原料多少克?
原料多少克?
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
【题目】某校为了解九年级学生的视力情况,随机抽样调查了部分九年级学生的视力,以下是根据调查结果绘制的统计图表的一部分.
分组 | 视力 | 人数 |
A | 3.95≤x≤4.25 | 2 |
B | 4.25<x≤4.55 | |
C | 4.55<x≤4.85 | 20 |
D | 4.85<x≤5.15 | |
E | 5.15<x≤5.45 | 3 |
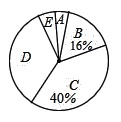
根据以上信息,解答下列问题:
(1)在被调查学生中,视力在3.95≤x≤4.25范围内的人数为 人,在4.25<x≤4.55范围内的学生数占被调查的学生数的百分比为 %.
(2)本次调查的样本容量是 ,视力在4.85<x≤5.15范围内的学生数占被调查学生数的百分比是 %.
(3)本次调查中,视力的中位数落在 组.
(4)若该校九年级有350名学生,估计视力超过4.85的学生数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,已知线段![]() ,以
,以![]() 为一边作等边
为一边作等边![]() (尺规作图,保留作图痕迹,不写作法);
(尺规作图,保留作图痕迹,不写作法);
(2)如图②,已知![]() ,
,![]() ,
,![]() ,分别以
,分别以![]() 为边作等边
为边作等边![]() 和等边
和等边![]() ,连接
,连接![]() ,求
,求![]() 的最大值;
的最大值;
(3)如图③,已知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 内部一点,连接
内部一点,连接![]() ,求出
,求出![]() 的最小值.
的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国宋朝数学家杨辉在他的著作《详解九章算法》中提出如图,此表揭示了(a+b)n(n为非负整数)展开式的各项系数的规律,例如:(a+b)0=1,它只有一项,系数为1;(a+b)1=a+b,它有两项,系数分别为1,1;(a+b)2=a2+2ab+b2,它有三项,系数分别为1,2,1;(a+b)3=a3+3a2b+3ab2+b3,它有四项,系数分别为1,3,3,1;…;根据以上规律,(a+b)5展开式共有六项,系数分别为______,拓展应用:(a﹣b)4=_______.
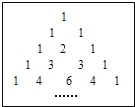
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】意大利文艺复兴时期的著名画家达芬奇利用两张一样的纸片拼出不一样的“空洞”,从而巧妙的证明了勾股定理.小明用两张全等的的纸片①和②拼成如图1所示的图形,中间的六边形![]() 由两个正方形和两个全等的直角三角形组成.已知六边形
由两个正方形和两个全等的直角三角形组成.已知六边形![]() 的面积为28,
的面积为28,![]() .小明将纸片②翻转后拼成如图2所示的图形,其中
.小明将纸片②翻转后拼成如图2所示的图形,其中![]() ,则四边形
,则四边形![]() 的面积为( )
的面积为( )

A.16B.20C.22D.24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN周长取最小值时,则∠MPN的度数为( )

A. 140° B. 100° C. 50° D. 40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在等边三角形![]() 中,
中,

①如图①,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的点,且
上的点,且![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,则
,则![]() 的度数是___________度;
的度数是___________度;
②如图②,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 延长线上的点,且
延长线上的点,且![]() ,
,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,此时
,此时![]() 的度数是____________度;
的度数是____________度;
(2)如图③,在![]() 中,
中,![]() ,
,![]() 是锐角,点
是锐角,点![]() 是
是![]() 边的垂直平分线与
边的垂直平分线与![]() 的交点,点
的交点,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 的延长线上,且
的延长线上,且![]() ,
,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,若
,若![]() ,求
,求![]() 的大小(用含法
的大小(用含法![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,等边△ABC的边长为3,分别以顶点B、A、C为圆心,BA长为半径作弧AC、弧CB、弧BA,我们把这三条弧所组成的图形称作莱洛三角形,显然莱洛三角形仍然是轴对称图形.设点I为对称轴的交点,如图2,将这个图形的顶点A与等边△DEF的顶点D重合,且AB⊥DE,DE=2π,将它沿等边△DEF的边作无滑动的滚动,当它第一次回到起始位置时,这个图形在运动中扫过区域面积是( )
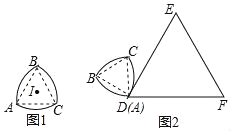
A. 18π B. 27π C. ![]() π D. 45π
π D. 45π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂准备在春节前生产甲、乙两种型号的新年礼盒共 80 万套,两种礼盒的成本和售价如下表所示;
甲 | 乙 | |
成本(元/套) | 25 | 28 |
售价(元/套) | 30 | 38 |
(1)该工厂计划筹资金 2150 万元,且全部用于生产甲乙两种礼盒,则这两种礼盒各生产多少万套?
(2)经过市场调查,该厂决定在原计划的基础上增加生产甲种礼盒![]() 万套,增加生产乙种礼盒
万套,增加生产乙种礼盒![]() 万套(
万套(![]() ,
,![]() 都为正整数),且两种礼盒售完后所获得的总利润恰为 690 万元,请问该工厂有几种生产方案?并写出所有可行的生产方案.
都为正整数),且两种礼盒售完后所获得的总利润恰为 690 万元,请问该工厂有几种生产方案?并写出所有可行的生产方案.
(3)在(2)的情况下,设实际生产的两种礼盒的总成本为![]() 万元,请写出
万元,请写出![]() 与
与![]() 的函数关系式,并求出当
的函数关系式,并求出当 ![]() 为多少时成本
为多少时成本![]() 有最小值,并求出成本
有最小值,并求出成本![]() 的最小值为多少万元?
的最小值为多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com