
【题目】(1)在等边三角形![]() 中,
中,

①如图①,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的点,且
上的点,且![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,则
,则![]() 的度数是___________度;
的度数是___________度;
②如图②,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 延长线上的点,且
延长线上的点,且![]() ,
,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,此时
,此时![]() 的度数是____________度;
的度数是____________度;
(2)如图③,在![]() 中,
中,![]() ,
,![]() 是锐角,点
是锐角,点![]() 是
是![]() 边的垂直平分线与
边的垂直平分线与![]() 的交点,点
的交点,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 的延长线上,且
的延长线上,且![]() ,
,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,若
,若![]() ,求
,求![]() 的大小(用含法
的大小(用含法![]() 的代数式表示).
的代数式表示).
【答案】(1)60;(2)60;(3)![]()
【解析】
(1)①只要证明△ACE≌△CBD,可得∠ACE=∠CBD,推出∠BFE=∠CBD+∠BCF=∠ACE+∠BCF=∠BCA=60°;
②只要证明△ACE≌△CBD,可得∠ACE=∠CBD=∠DCF,即可推出∠BFE=∠D+∠DCF=∠D+∠CBD=∠BCA=60°;
(2)只要证明△AEC≌△CDB,可得∠E=∠D,即可推出∠BFE=∠D+∠DCF=∠E+∠ECA=∠OAC=α.
解:(1)①如图①中,
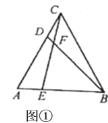
∵△ABC是等边三角形,
∴AC=CB,∠A=∠BCD=60°,
∵AE=CD,
∴△ACE≌△CBD,
∴∠ACE=∠CBD,
∴∠BFE=∠CBD+∠BCF=∠ACE+∠BCF=∠BCA=60°.
故答案为60;
②如图②,
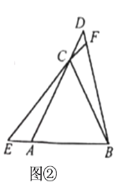
∵△ABC是等边三角形,
∴AC=CB,∠A=∠BCD=60°,
∴∠CAE=∠BCD=′120°
∵AE=CD,
∴△ACE≌△CBD,
∴∠ACE=∠CBD=∠DCF,
∴∠BFE=∠D+∠DCF=∠D+∠CBD=∠BCA=60°.
故答案为60;
(2)如图③中,
图③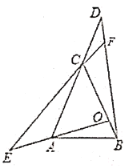
![]() 点
点![]() 是
是![]() 边的垂直平分线与
边的垂直平分线与![]() 的交点,
的交点,
![]() ,
,
![]()
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.


科目:初中数学 来源: 题型:
【题目】(1)探究新知:如图1,已知△ABC与△ABD的面积相等,试判断AB与CD的位置关系,并说明理由.

(2)结论应用:① 如图2,点M,N在反比例函数![]() (k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.试证明:MN∥EF.
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.试证明:MN∥EF.
② 若①中的其他条件不变,只改变点M,N的位置如图3所示,请判断 MN与EF是否平行?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某甜品店用![]() ,
,![]() 两种原料制作成甲、乙两款甜品进行销售,制作每份甜品的原料所需用量如下表所示.该店制作甲款甜品
两种原料制作成甲、乙两款甜品进行销售,制作每份甜品的原料所需用量如下表所示.该店制作甲款甜品![]() 份,乙款甜品
份,乙款甜品![]() 份,共用去
份,共用去![]() 原料2000克.
原料2000克.
原料 款式 |
(克) |
(克) |
甲款甜品 | 30 | 15 |
乙款甜品 | 10 | 20 |
(1)求![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)已知每份甲甜品的利润为5元,每份乙甜品的利润为2元.假设两款甜品均能全部卖出.若获得总利润不少于360元,则至少要用去![]() 原料多少克?
原料多少克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC的边长为6,在AC,BC边上各取一点E,F,使AE=CF,连接AF、BE相交于点P,当点E从点A运动到点C时,点P经过点的路径长为__.
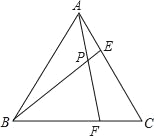
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在正方形ABCD中,点E与点F分别在线段AC、BC上,且四边形DEFG是正方形.


(1)试探究线段AE与CG的关系,并说明理由.
(2)如图②若将条件中的四边形ABCD与四边形DEFG由正方形改为矩形,AB=3,BC=4.
①线段AE、CG在(1)中的关系仍然成立吗?若成立,请证明,若不成立,请写出你认为正确的关系,并说明理由.
②当△CDE为等腰三角形时,求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
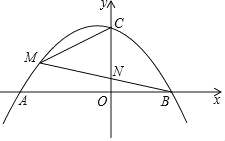
【题目】如图,抛物线y=ax2+ax﹣12a(a<0)与x轴交于A、B两点(A在B的左侧),与y轴交于点C,点M是第二象限内抛物线上一点,BM交y轴于N.
(1)求点A、B的坐标;
(2)若BN=MN,且S△MBC=![]() ,求a的值;
,求a的值;
(3)若∠BMC=2∠ABM,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解黔东南州某县2013届中考学生的体育考试得分情况,从该县参加体育考试的4000名学生中随机抽取了100名学生的体育考试成绩作样本分析,得出如下不完整的频数统计表和频数分布直方图.
成绩分组 | 组中值 | 频数 |
25≤x<30 | 27.5 | 4 |
30≤x<35 | 32.5 | m |
35≤x<40 | 37.5 | 24 |
40≤x<45 | a | 36 |
45≤x<50 | 47.5 | n |
50≤x<55 | 52.5 | 4 |
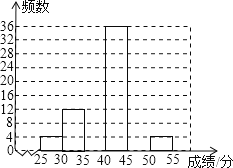
(1)求a、m、n的值,并补全频数分布直方图;
(2)若体育得分在40分以上(包括40分)为优秀,请问该县中考体育成绩优秀学生人数约为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com