
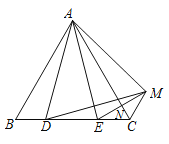
【题目】如图,在等边![]() 中,
中,![]() ,将线段
,将线段![]() 沿
沿![]() 翻折,得到线段
翻折,得到线段![]() ,连结
,连结![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() 、
、![]() 以下说法:①
以下说法:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 中,正确的有( )
中,正确的有( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
【答案】D
【解析】
由△ABD≌△ACE,△ACE≌△ACM,△ABC是等边三角形可以对①②进行判断,由AC垂直平分EM和直角三角形的性质可对③进行判断,由△ADM是等边三角形可对④进行判断.
解:∵△ABC是等边三角形,
∴AB=AC,∠B=∠BAC=∠ACB=60°,
∵BD=CE,
∴△ABD≌△ACE(SAS)
∴AD=AE,∠BAD=∠CAE
∵线段![]() 沿
沿![]() 翻折,
翻折,
∴AE=AM,∠CAE=∠CAM,
∴![]() ,故①正确,
,故①正确,
∴△ACE≌△ACM(SAS)
∴∠ACE=∠ACM=60°,故②正确,
由轴对称的性质可知,AC垂直平分EM,
∴∠CNE=∠CNM=90°,
∵∠ACM =60°,
∴∠CMN=30°,
∴在Rt△CMN中,![]() ,即
,即![]() ,故③正确,
,故③正确,
∵∠BAD=∠CAE,∠CAE=∠CAM,
∴∠BAD=∠CAM,
∵∠∠BAD+∠CAD=60°,
∴∠CAM +∠CAD=60°,
即∠DAM=60°,又AD=AM
∴△ADM为等边三角形,
∴![]() 故④正确,
故④正确,
所以正确的有4个,
故答案为:D.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】一辆客车从甲地开住乙地,一辆出租车从乙地开往甲地,两车同时出发,两车距甲地的距离y(千米)与行驶时间式(小时)之间的函数图象如图所示,则下列说法中错误的是( )
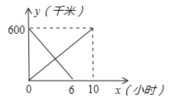
A. 客车比出租车晚4小时到达目的地B. 客车速度为60千米时,出租车速度为100千米/时
C. 两车出发后3.75小时相遇D. 两车相遇时客车距乙地还有225千米
查看答案和解析>>
科目:初中数学 来源: 题型:
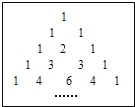
【题目】我国宋朝数学家杨辉在他的著作《详解九章算法》中提出如图,此表揭示了(a+b)n(n为非负整数)展开式的各项系数的规律,例如:(a+b)0=1,它只有一项,系数为1;(a+b)1=a+b,它有两项,系数分别为1,1;(a+b)2=a2+2ab+b2,它有三项,系数分别为1,2,1;(a+b)3=a3+3a2b+3ab2+b3,它有四项,系数分别为1,3,3,1;…;根据以上规律,(a+b)5展开式共有六项,系数分别为______,拓展应用:(a﹣b)4=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN周长取最小值时,则∠MPN的度数为( )

A. 140° B. 100° C. 50° D. 40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在等边三角形![]() 中,
中,

①如图①,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的点,且
上的点,且![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,则
,则![]() 的度数是___________度;
的度数是___________度;
②如图②,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 延长线上的点,且
延长线上的点,且![]() ,
,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,此时
,此时![]() 的度数是____________度;
的度数是____________度;
(2)如图③,在![]() 中,
中,![]() ,
,![]() 是锐角,点
是锐角,点![]() 是
是![]() 边的垂直平分线与
边的垂直平分线与![]() 的交点,点
的交点,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 的延长线上,且
的延长线上,且![]() ,
,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,若
,若![]() ,求
,求![]() 的大小(用含法
的大小(用含法![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,等边△ABC的边长为3,分别以顶点B、A、C为圆心,BA长为半径作弧AC、弧CB、弧BA,我们把这三条弧所组成的图形称作莱洛三角形,显然莱洛三角形仍然是轴对称图形.设点I为对称轴的交点,如图2,将这个图形的顶点A与等边△DEF的顶点D重合,且AB⊥DE,DE=2π,将它沿等边△DEF的边作无滑动的滚动,当它第一次回到起始位置时,这个图形在运动中扫过区域面积是( )
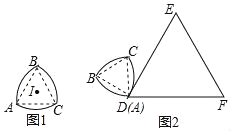
A. 18π B. 27π C. ![]() π D. 45π
π D. 45π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国移动某套餐推出了如下两种流量计费方式:
月租费/元 | 流量费(元/ | |
方式一 | 8 | 1 |
方式二 | 28 | 0.5 |
(1)设一个月内用移动电话使用流量为![]() ,方式一总费用
,方式一总费用![]() 元,方式二总费用
元,方式二总费用![]() 元(总费用不计通话费及其它服务费).写出
元(总费用不计通话费及其它服务费).写出![]() 和
和![]() 关于
关于![]() 的函数关系式(不要求写出自变量
的函数关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
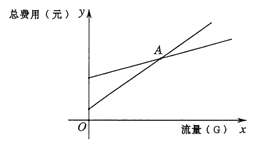
(2)如图为在同一平面直角坐标系中画出(1)中的两个函数图象的示意图,记它们的交点为点![]() ,求点
,求点![]() 的坐标,并解释点
的坐标,并解释点![]() 坐标的实际意义;
坐标的实际意义;
(3)根据(2)中函数图象,结合每月使用的流量情况,请直接写出选择哪种计费方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=﹣x2+bx+c(b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.

(1)求该二次函数的解析式及点M的坐标;
(2)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围;
(3)点P是直线AC上的动点,若点P,点C,点M所构成的三角形与△BCD相似,请直接写出所有点P的坐标(直接写出结果,不必写解答过程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com