
����Ŀ���й��ƶ�ij�ײ��Ƴ����������������Ʒѷ�ʽ��
�����/Ԫ | �����ѣ�Ԫ/ | |
��ʽһ | 8 | 1 |
��ʽ�� | 28 | 0.5 |
��1����һ���������ƶ��绰ʹ������Ϊ![]() ����ʽһ�ܷ���
����ʽһ�ܷ���![]() Ԫ����ʽ���ܷ���
Ԫ����ʽ���ܷ���![]() Ԫ���ܷ��ò���ͨ���Ѽ���������ѣ���д��
Ԫ���ܷ��ò���ͨ���Ѽ���������ѣ���д��![]() ��
��![]() ����
����![]() �ĺ�����ϵʽ����Ҫ��д���Ա���
�ĺ�����ϵʽ����Ҫ��д���Ա���![]() ��ȡֵ��Χ����
��ȡֵ��Χ����
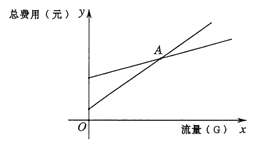
��2����ͼΪ��ͬһƽ��ֱ������ϵ�л�����1���е���������ͼ���ʾ��ͼ�������ǵĽ���Ϊ��![]() �����
�����![]() �����꣬�����͵�
�����꣬�����͵�![]() �����ʵ�����壻
�����ʵ�����壻
��3�����ݣ�2���к���ͼ���ÿ��ʹ�õ������������ֱ��д��ѡ�����ּƷѷ�ʽ�����㣮
���𰸡���1��![]() ��
��![]() ����2����A��������40��48������3����������
����2����A��������40��48������3����������
��������
��1�����ݱ������շѷ�ʽ�ͺ���ͼ���ɵó���������ʽ��
��2������������������ʽ�����ɵó��佻������A����ʵ�����弴Ϊ��ÿ��ʹ�õ�����Ϊ40Gʱ�����ּƷѷ�ʽ���ܷ���һ���࣬��Ϊ48Ԫ��
��3����Ϻ���ͼ�����������ݽ�������ֶ����ۼ���.
��1�����ݱ����ɵ�![]() ��
��
![]() ��
��
��2��������ã�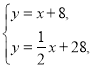
��֮����![]()
����A��������40��48����
��A�������ʵ������Ϊ��ÿ��ʹ�õ�����Ϊ40Gʱ�����ּƷѷ�ʽ���ܷ���һ���࣬��Ϊ48Ԫ��
��3����ÿ��ʹ�õ���������40Gʱ��ѡ��ʽһ��ʡǮ��
��ÿ��ʹ�õ���������40Gʱ�����ַ�ʽ���ܷ��ö�һ����
��ÿ��ʹ�õ���������40Gʱ��ѡ��ʽ����ʡǮ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
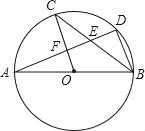
����Ŀ����ͼ��AB����O��ֱ����C��D����O�ϵĵ㣬��OC��BD��AD�ֱ���BC��OC�ཻ�ڵ�E��F�������н��ۣ���AD��BD���ڡ�AOC=��AEC����CBƽ����ABD����AF=DF����BD=2OF���ޡ�CEF�ա�BED������һ��������____��������Ϊ��ȷ���۵���Ŷ����ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵȱ�![]() �У�
�У�![]() �����߶�
�����߶�![]() ��
��![]() ���ۣ��õ��߶�
���ۣ��õ��߶�![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() ����˵������
����˵������![]() ����
����![]() ����
����![]() ����
����![]() �У���ȷ���У� ��
�У���ȷ���У� ��
A.![]() ��B.
��B.![]() ��C.
��C.![]() ��D.
��D.![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Уѧ������ij����ͺ���������˲���ͬѧ�Ͳͷ��˵�ʣ��������������ͳ�ƺ���Ƴ�����ͼ��ʾ�IJ�������ͳ��ͼ��
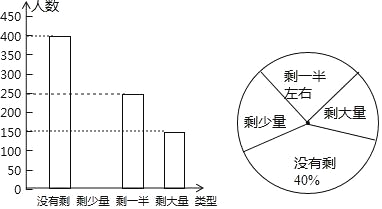
��1����α������ͬѧ��������
��2����ȫ����ͳ��ͼ��
��3������������ͳ��ͼ��ʣ������������Ӧ����Բ�ĽǵĶ�����
��4��Уѧ����ͨ�����ݷ�����������α����������ѧ��һ���˷ѵ�ʳ����Թ�200����һ�ͣ��ݴ˹��㣬��У20000��ѧ��һ���˷ѵ�ʳ��ɹ�������ʳ��һ�ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
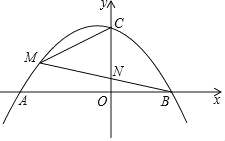
����Ŀ����ͼ��������y=ax2+ax��12a��a��0����x�ύ��A��B���㣨A��B����ࣩ����y�ύ�ڵ�C����M�ǵڶ���������������һ�㣬BM��y����N��
��1�����A��B�����ꣻ
��2����BN=MN����S��MBC=![]() ����a��ֵ��
����a��ֵ��
��3������BMC=2��ABM����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
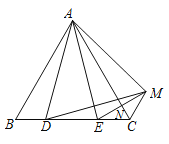
����Ŀ����ͼ��������ABCD�У�AB=BD����E��F�ֱ���AB��AD������ĵ㣨����˵��غϣ�����AE=DF������BF��DE�ཻ�ڵ�G������CG��BD�ཻ�ڵ�H���������¼������ۣ�
�١�ADE=��DBF���ڡ�DAE�ա�BDG������AF=2DF����BG=6GF����CG��BDһ������ֱ���ݡ�BGE=60����������ȷ�Ľ��۸���Ϊ��������
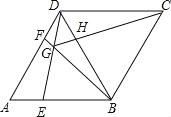
A. 5 B. 4 C. 3 D. 2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ����������������������Ϊһ����Ŀ����A��B���ֵ��ߣ���80���� �����ĵ�����Ҫ�ס������ֲ�����϶��ɣ����м��ֲ���700�������ֲ���500������֪��װA��B���ֵ�������ļס������ֲ��ϣ����±���ʾ��
���ֲ��ϣ����� | ���ֲ��ϣ����� | |
A���� | 6 | 8 |
B���� | 10 | 4 |
�������㣬����һ��A���ߵķ���Ϊ5Ԫ��һ��B���ߵķ���Ϊ4.5Ԫ�� ����װA�ֵ���x���������ܷ���ΪyԪ��
��1����y��x�ĺ�����ϵʽ�������x��ȡֵ��Χ��
��2������װA�ֵ��߶��ٸ�ʱ�������ܷ������٣����ٷ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ�
С����������һ�����⣺
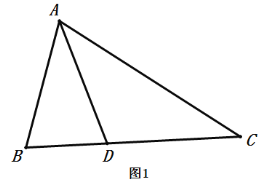
��ͼ1����![]() �У�
�У�![]() ƽ��
ƽ��![]() ��
��![]() ����֤��
����֤��![]()
С��ͨ��˼�����֣�����ͨ�����س������̡����ַ���������⣺
����1����ͼ2����![]() �Ͻ�ȡ
�Ͻ�ȡ![]() ��ʹ��
��ʹ��![]() ������
������![]() �����Եõ�ȫ�������Σ������������
�����Եõ�ȫ�������Σ������������
����������ͼ3���ӳ�![]() ����
����![]() ��ʹ��
��ʹ��![]() ������
������![]() �����Եõ����������Σ������������
�����Եõ����������Σ������������
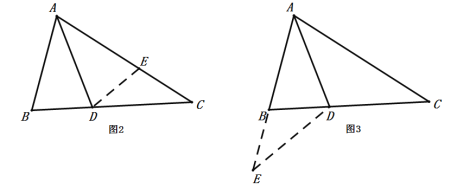
��1�������Ķ����ϣ���ѡһ�ַ���֤��![]()
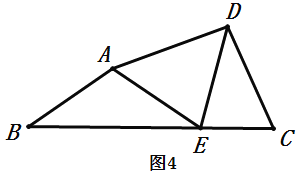
��2�������Լ��Ľ��⾭���ο�С���ķ����������������⣺��ͼ4���ı���![]() �У�
��![]() ��
��![]() ��һ�㣬
��һ�㣬![]() ��
��![]() ��
��![]() ��̽��
��̽��![]() ��
��![]() ��
��![]() ֮���������ϵ����֤��
֮���������ϵ����֤��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
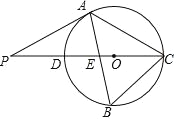
����Ŀ����ͼ����ABC�ڽ��ڡ�O��CD�ǡ�O��ֱ����AB��CD���ڵ�E����P��CD�ӳ����ϵ�һ�㣬AP=AC���ҡ�B=2��P��
��1����֤��PA�ǡ�O�����ߣ�
��2����PD=![]() �����O��ֱ����
�����O��ֱ����
��3���ڣ�2���������£�����B�ȷְ�ԲCD����DE�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com