
【题目】某中学决定在“五·四艺术周”为一个节目制作A、B两种道具,共80个. 制作的道具需要甲、乙两种材料组合而成,现有甲种材料700件,乙种材料500件,已知组装A、B两种道具所需的甲、乙两种材料,如下表所示:
甲种材料(件) | 乙种材料(件) | |
A道具 | 6 | 8 |
B道具 | 10 | 4 |
经过计算,制作一个A道具的费用为5元,一个B道具的费用为4.5元. 设组装A种道具x个,所需总费用为y元.
(1)求y与x的函数关系式,并求出x的取值范围;
(2)问组装A种道具多少个时,所需总费用最少,最少费用是多少?
【答案】(1)y = 0.5x + 360, 25≤x≤45;(2)当组装A道具25个时,所花费用最少,最少费用是372.5元
【解析】
(1)设组装A种道具x个,则B种道具(80﹣x)个,根据“总费用=A种道具费用+B种道具费用”即可得出y与x的函数关系式;再根据题意列不等式组即可得出x的取值范围;
(2)根据(1)的结论,结合一次函数的性质解答即可.
(1)设组装A种道具x个,则B种道具(80﹣x)个,根据题意得:
y = 5x + 4.5(80-x)
= 0.5x + 360
根据题意,得:
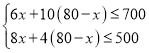
解得25≤x≤45.
∴ x的取值范围是25≤x≤45.
(2)由(1)得,y=0.5x+360,
∵y是x的一次函数,且0.5>0,
∴y随着x的增大而增大,
∴当x=25时,y最小=0.5×25+360=372.5
答:当组装A道具25个时,所花费用最少,最少费用是372.5元.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
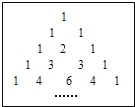
【题目】我国宋朝数学家杨辉在他的著作《详解九章算法》中提出如图,此表揭示了(a+b)n(n为非负整数)展开式的各项系数的规律,例如:(a+b)0=1,它只有一项,系数为1;(a+b)1=a+b,它有两项,系数分别为1,1;(a+b)2=a2+2ab+b2,它有三项,系数分别为1,2,1;(a+b)3=a3+3a2b+3ab2+b3,它有四项,系数分别为1,3,3,1;…;根据以上规律,(a+b)5展开式共有六项,系数分别为______,拓展应用:(a﹣b)4=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,等边△ABC的边长为3,分别以顶点B、A、C为圆心,BA长为半径作弧AC、弧CB、弧BA,我们把这三条弧所组成的图形称作莱洛三角形,显然莱洛三角形仍然是轴对称图形.设点I为对称轴的交点,如图2,将这个图形的顶点A与等边△DEF的顶点D重合,且AB⊥DE,DE=2π,将它沿等边△DEF的边作无滑动的滚动,当它第一次回到起始位置时,这个图形在运动中扫过区域面积是( )
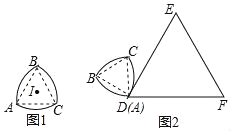
A. 18π B. 27π C. ![]() π D. 45π
π D. 45π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国移动某套餐推出了如下两种流量计费方式:
月租费/元 | 流量费(元/ | |
方式一 | 8 | 1 |
方式二 | 28 | 0.5 |
(1)设一个月内用移动电话使用流量为![]() ,方式一总费用
,方式一总费用![]() 元,方式二总费用
元,方式二总费用![]() 元(总费用不计通话费及其它服务费).写出
元(总费用不计通话费及其它服务费).写出![]() 和
和![]() 关于
关于![]() 的函数关系式(不要求写出自变量
的函数关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
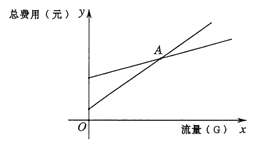
(2)如图为在同一平面直角坐标系中画出(1)中的两个函数图象的示意图,记它们的交点为点![]() ,求点
,求点![]() 的坐标,并解释点
的坐标,并解释点![]() 坐标的实际意义;
坐标的实际意义;
(3)根据(2)中函数图象,结合每月使用的流量情况,请直接写出选择哪种计费方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知经过点M(1,4)的直线y = kx+b(k≠0)与直线y = 2x-3平行.
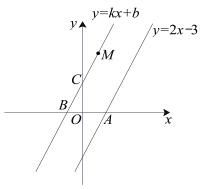
(1)求k,b的值;
(2)若直线y = 2x-3与x轴交于点A,直线y = kx+b交x轴于点B,交y轴于点C,求△MAC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市出租车计费办法如图所示.根据图象信息,下列说法错误的是( )
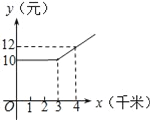
A. 出租车起步价是10元
B. 在3千米内只收起步价
C. 超过3千米部分(x>3)每千米收3元
D. 超过3千米时(x>3)所需费用y与x之间的函数关系式是y=2x+4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂准备在春节前生产甲、乙两种型号的新年礼盒共 80 万套,两种礼盒的成本和售价如下表所示;
甲 | 乙 | |
成本(元/套) | 25 | 28 |
售价(元/套) | 30 | 38 |
(1)该工厂计划筹资金 2150 万元,且全部用于生产甲乙两种礼盒,则这两种礼盒各生产多少万套?
(2)经过市场调查,该厂决定在原计划的基础上增加生产甲种礼盒![]() 万套,增加生产乙种礼盒
万套,增加生产乙种礼盒![]() 万套(
万套(![]() ,
,![]() 都为正整数),且两种礼盒售完后所获得的总利润恰为 690 万元,请问该工厂有几种生产方案?并写出所有可行的生产方案.
都为正整数),且两种礼盒售完后所获得的总利润恰为 690 万元,请问该工厂有几种生产方案?并写出所有可行的生产方案.
(3)在(2)的情况下,设实际生产的两种礼盒的总成本为![]() 万元,请写出
万元,请写出![]() 与
与![]() 的函数关系式,并求出当
的函数关系式,并求出当 ![]() 为多少时成本
为多少时成本![]() 有最小值,并求出成本
有最小值,并求出成本![]() 的最小值为多少万元?
的最小值为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=﹣x2+bx+c(b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.

(1)求该二次函数的解析式及点M的坐标;
(2)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围;
(3)点P是直线AC上的动点,若点P,点C,点M所构成的三角形与△BCD相似,请直接写出所有点P的坐标(直接写出结果,不必写解答过程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com