
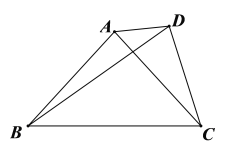
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 和点
和点![]() 在直线
在直线![]() 的同侧,
的同侧,![]() ,连接
,连接![]() ,则
,则![]() 的度数为__________.
的度数为__________.
【答案】30°
【解析】
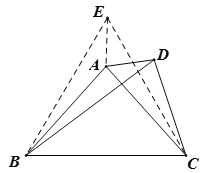
先根据等腰三角形的性质和三角形的内角和定理以及角的和差求出![]() 的度数,然后作点D关于直线AB的对称点E,连接BE、CE、AE,如图,则BE=BD,∠EBA=∠DB,∠BEA=∠BDA,进而可得∠EBC=60°,由于BD=BC,从而可证△EBC是等边三角形,可得∠BEC=60°,EB=EC,进一步即可根据SSS证明△AEB≌△AEC,可得∠BEA的度数,问题即得解决.
的度数,然后作点D关于直线AB的对称点E,连接BE、CE、AE,如图,则BE=BD,∠EBA=∠DB,∠BEA=∠BDA,进而可得∠EBC=60°,由于BD=BC,从而可证△EBC是等边三角形,可得∠BEC=60°,EB=EC,进一步即可根据SSS证明△AEB≌△AEC,可得∠BEA的度数,问题即得解决.
解:∵![]() ,
,![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
作点D关于直线AB的对称点E,连接BE、CE、AE,如图,则BE=BD,∠EBA=∠DBA=11°,∠BEA=∠BDA,
∴∠EBC=11°+11°+38°=60°,
∵BD=BC,∴BE=BC,∴△EBC是等边三角形,∴∠BEC=60°,EB=EC,
又∵AB=AC,EA=EA,
∴△AEB≌△AEC(SSS),∴∠BEA=∠CEA=![]() ,
,
∴∠ADB=30°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某中学决定在“五·四艺术周”为一个节目制作A、B两种道具,共80个. 制作的道具需要甲、乙两种材料组合而成,现有甲种材料700件,乙种材料500件,已知组装A、B两种道具所需的甲、乙两种材料,如下表所示:
甲种材料(件) | 乙种材料(件) | |
A道具 | 6 | 8 |
B道具 | 10 | 4 |
经过计算,制作一个A道具的费用为5元,一个B道具的费用为4.5元. 设组装A种道具x个,所需总费用为y元.
(1)求y与x的函数关系式,并求出x的取值范围;
(2)问组装A种道具多少个时,所需总费用最少,最少费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
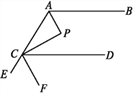
【题目】如图,AP,CP分别平分∠BAC,∠ACD,∠P=90°,设∠BAP=α.
(1)用α表示∠ACP;
(2)求证:AB∥CD;
(3)若AP∥CF,求证:FC平分∠DCE.
查看答案和解析>>
科目:初中数学 来源: 题型:
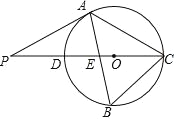
【题目】如图,△ABC内接于⊙O,CD是⊙O的直径,AB与CD交于点E,点P是CD延长线上的一点,AP=AC,且∠B=2∠P.
(1)求证:PA是⊙O的切线;
(2)若PD=![]() ,求⊙O的直径;
,求⊙O的直径;
(3)在(2)的条件下,若点B等分半圆CD,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为
为![]() 轴上一个动点,
轴上一个动点,![]()
(1)如图1,当![]() ,且
,且![]() 按逆时针方向排列,求
按逆时针方向排列,求![]() 点的坐标.
点的坐标.
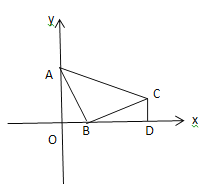
(图1)
(2)如图2,当![]() ,且
,且![]() 按顺时针方向排列,
按顺时针方向排列,![]() 连
连![]() 交
交![]() 轴于
轴于![]() ,求证:
,求证:![]()
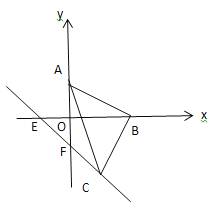
(图2)
(3)如图3,m>2,且![]() 按顺时针方向排列,若
按顺时针方向排列,若![]() 两点关于直线
两点关于直线![]() 的的对称点,画出图形并用含
的的对称点,画出图形并用含![]() 的式子表示
的式子表示![]() 的面积
的面积![]()
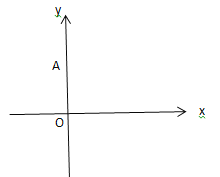
图3
查看答案和解析>>
科目:初中数学 来源: 题型:
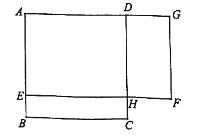
【题目】如图, ![]() 是一块边长为4米的正方形苗圃,园林部门将其改造为矩形
是一块边长为4米的正方形苗圃,园林部门将其改造为矩形![]() 的形状,其中点
的形状,其中点![]() 在
在![]() 边上,点
边上,点![]() 在
在![]() 的延长线上,
的延长线上, ![]() 设
设![]() 的长为
的长为![]() 米,改造后苗圃
米,改造后苗圃![]() 的面积为
的面积为![]() 平方米.
平方米.
(1) ![]() 与
与![]() 之间的函数关系式为 (不需写自变量的取值范围);
之间的函数关系式为 (不需写自变量的取值范围);
(2)根据改造方案,改造后的矩形苗圃![]() 的面积与原正方形苗圃
的面积与原正方形苗圃![]() 的面积相等,请问此时
的面积相等,请问此时![]() 的长为多少米?
的长为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=x2+mx+n与x轴正半轴交于A,B两点(点A在点B左侧),与y轴交于点C.
(1)利用直尺和圆规,作出抛物线y=x2+mx+n的对称轴(尺规作图,保留作图痕迹,不写作法);
(2)若△OBC是等腰直角三角形,且其腰长为3,求抛物线的解析式;
(3)在(2)的条件下,点P为抛物线对称轴上的一点,则PA+PC的最小值为 .
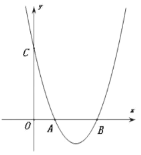
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形外,使OK边与AB边重合,如图所示,按下列步骤操作:将正方形在正六边形外绕点B逆时针旋转,使ON边与BC边重合,完成第一次旋转;再绕点C逆时针旋转,使MN边与CD边重合,完成第二次旋转;……在这样连续6次旋转的过程中,点B,O间的距离不可能是( )
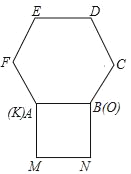
A. 0 B. 0.8 C. 2.5 D. 3.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,AB=1,BC=2,∠B=45°,M为AB的中点.
(1)求tan∠CMD的值;
(2)设N为CD中点,CM交BN于K,求![]() 及S△BKC的值.
及S△BKC的值.
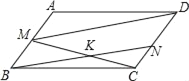
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com