
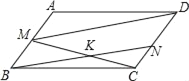
【题目】在ABCD中,AB=1,BC=2,∠B=45°,M为AB的中点.
(1)求tan∠CMD的值;
(2)设N为CD中点,CM交BN于K,求![]() 及S△BKC的值.
及S△BKC的值.
【答案】(1)tan∠CMD=![]() ;(2)
;(2)![]() ,
,![]() .
.
【解析】
(1)过点M作MF⊥BC于F,交DA的延长线于E,作DG⊥MC交MC的延长线
于G,①求出ME,MF,BF的长,②求出MC的长,③求出ABCD的面积,△MCD的面
积,④由△MCD的面积,求出DG的长,⑤由勾股定理求出CG的长,⑥求出MG的长,
⑦在Rt△MDG中,求出tan∠CMD的值.
(2)易证明△KBM≌△KNC,∴BK=BN,∴![]()
![]()
解:(1)过点M作MF⊥BC于F,交DA的延长线于E,作DG⊥MC交MC的延长线于G,
∵在ABCD中,AB=1,BC=2,∠B=45°,M为AB的中点.
∴BM=AM=![]() ,∠EAM=∠B=45°,
,∠EAM=∠B=45°,
∴△AEM、△BFM是等腰直角三角形,
∴AE=EM=BF=MF=![]()
∴![]()
∴![]()
∵AE=EM=BF=MF=![]()
∴EF=EM+FM=![]()
∴SABCD=ADEF=![]() ,
,
∵点M是AB的中点,
∴![]()
∵![]()
∴![]()
在Rt△CDG中,由勾股定理得:
![]()
∴
![]()
在Rt△MDG中,
tan∠CMD=![]()

(2)在ABCD中,M为AB的中点,N为CD中点,
∴BM=CN,
∵AB∥CD,
∴∠MBK=∠CNK,∠BMK=NCK,
在△BMK和△NCK中,

∴△BMK≌△NCK(ASA)
∴BK=NK,MK=CK,
∴![]()
∵MK=CK,
∴![]()


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,己知抛物线经过点A(l, 0),B(一3,0),C(0,3)三点.
(1)求抛物线的解析式;
(2)在x轴下方的抛物线上,是否存在点M,使得![]() ?若存在求出M点的坐标;若不存在,请说明理由;
?若存在求出M点的坐标;若不存在,请说明理由;
(3)点P是位于直线BC上方的抛物线上的一个动点,是否存在点P,使![]() 的面积最大?若存在,求出P的坐标及
的面积最大?若存在,求出P的坐标及![]() 的最大值:若不存在,说明理由.
的最大值:若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
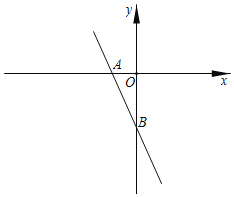
【题目】如图,在平面直角坐标系中,一次函数y=﹣2x﹣2交x轴于点A,交y轴于点B,若直线BC交x轴于点C,且∠ABC=45°,则点C的横坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线y=![]() x+b与x轴交于点A,与y轴交于点B,点P坐标为(3,0),过点P作PC⊥x轴于P,且△ABC为等腰直角三角形.
x+b与x轴交于点A,与y轴交于点B,点P坐标为(3,0),过点P作PC⊥x轴于P,且△ABC为等腰直角三角形.
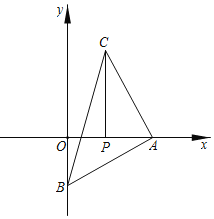
(1)如图,当∠BAC=90°,AB=AC时,求证△ABO≌△CAP;
(2)当AB为直角边时,请直接写出所有可能的b值.
查看答案和解析>>
科目:初中数学 来源: 题型:
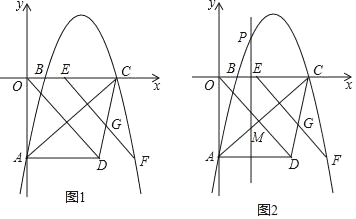
【题目】如图1,已知抛物线y=﹣![]() x2+
x2+![]() x﹣4与y轴相交于点A,与x轴相交于B和点C(点C在点B的右侧,点D的坐标为(4,﹣4),将线段OD沿x轴的正方向平移n个单位后得到线段EF.
x﹣4与y轴相交于点A,与x轴相交于B和点C(点C在点B的右侧,点D的坐标为(4,﹣4),将线段OD沿x轴的正方向平移n个单位后得到线段EF.
(1)当n= 时,点E或点F正好移动到抛物线上;
(2)当点F正好移动到抛物线上,EF与CD相交于点G时,求GF的长;
(3)如图2,若点P是x轴上方抛物线上一动点,过点P作平行于y轴的直线交AC于点M,探索是否存在点P,使线段MP长度有最大值?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
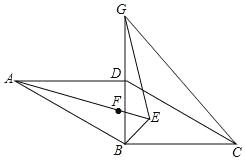
【题目】如图,在ABCD中,BD⊥BC,∠BDC=60°,∠DAB和∠DBC的平分线相交于点E,F为AE上一点,EF=EB,G为BD延长线上一点,BG=AB,连接GE.
(1)若ABCD的面积为9![]() ,求AB的长;
,求AB的长;
(2)求证:AF=GE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中,![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,过点
,过点![]() 画
画![]() 交直线
交直线![]() 于
于![]() (即点
(即点![]() 的纵坐标始终为
的纵坐标始终为![]() ),连接
),连接![]() .
.
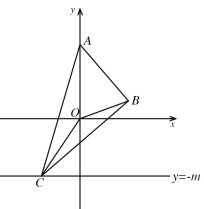
(1)求![]() 的长.
的长.
(2)若![]() 为等腰直角三角形,求
为等腰直角三角形,求![]() 的值.
的值.
(3)在(2)的条件下求![]() 所在直线的表达式.
所在直线的表达式.
(4)用![]() 的代数式表示
的代数式表示![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com