
【题目】如图1,已知抛物线y=﹣![]() x2+
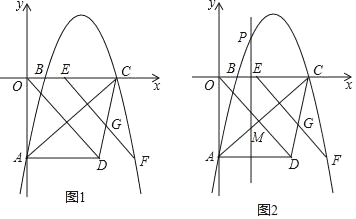
x2+![]() x﹣4与y轴相交于点A,与x轴相交于B和点C(点C在点B的右侧,点D的坐标为(4,﹣4),将线段OD沿x轴的正方向平移n个单位后得到线段EF.
x﹣4与y轴相交于点A,与x轴相交于B和点C(点C在点B的右侧,点D的坐标为(4,﹣4),将线段OD沿x轴的正方向平移n个单位后得到线段EF.
(1)当n= 时,点E或点F正好移动到抛物线上;
(2)当点F正好移动到抛物线上,EF与CD相交于点G时,求GF的长;
(3)如图2,若点P是x轴上方抛物线上一动点,过点P作平行于y轴的直线交AC于点M,探索是否存在点P,使线段MP长度有最大值?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)1或2或5;(2)![]() ;(3)存在点P(
;(3)存在点P(![]() ,3),使线段MP长度有最大值为5.
,3),使线段MP长度有最大值为5.
【解析】
(1)分点E与点B重合,点E与点C重合,点F在抛物线上三种情况讨论,可求
n的值;
(2)由题意可求直线EF解析式,直线CD解析式,即可求点G坐标,根据两点距离公式
可求GF的长;
(3)由题意可求直线AC解析式,设点![]() ,则点
,则点![]() ,则可用
,则可用
t表示PM的长度,根据二次函数的性质可求点P的坐标.
(1)∵抛物线![]() 与x轴相交于B和点C
与x轴相交于B和点C
∴![]()
∴x1=1,x2=5
∴点B(1,0),点C(5,0)
当点E与点B重合,则n=1,
当点E与点C重合,则n=5
当点F在抛物线上,则![]()
解得:x1=0(不合题意舍去),x2=6
∴F(6,﹣4)
∴n=6﹣4=2
故答案为:1或2或5
(2)∵点F正好移动到抛物线上
∴n=2
∴点E坐标为(2,0)
∵点E(2,0),点F(6,﹣4)
∴直线EF解析式:y=﹣x+2
∵点C(5,0),点D(4,﹣4)
∴直线CD解析式:y=4x﹣20
设点G(x,y)
∵EF与CD相交于点G
∴![]()
解得: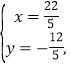
∴点![]() ,
,
∵点![]() ,点F(6,﹣4)
,点F(6,﹣4)
∴![]()
(3)存在点P,使线段MP长度有最大值
∵抛物线![]() 与y轴相交于点A,
与y轴相交于点A,
∴当x=0时,y=﹣4
∴点A(0,﹣4)
∵点A(0,﹣4),点C(5,0)
∴直线AC解析式:![]()
设点设点![]() ,则点
,则点![]() ,
,
∴![]()
∴当![]() 时,PM的最大值为5
时,PM的最大值为5
∴点P坐标为![]() ,
,
∴存在点P![]() ,使线段MP长度有最大值为5.
,使线段MP长度有最大值为5.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
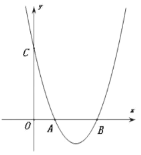
【题目】如图,在平面直角坐标系中,抛物线y=x2+mx+n与x轴正半轴交于A,B两点(点A在点B左侧),与y轴交于点C.
(1)利用直尺和圆规,作出抛物线y=x2+mx+n的对称轴(尺规作图,保留作图痕迹,不写作法);
(2)若△OBC是等腰直角三角形,且其腰长为3,求抛物线的解析式;
(3)在(2)的条件下,点P为抛物线对称轴上的一点,则PA+PC的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
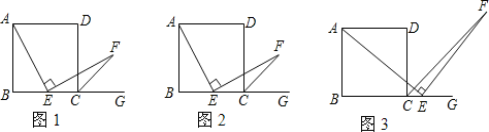
【题目】数学课上,张老师出示了问题:如图1,四边形ABCD是正方形,点E是边BC的中点.∠AEF=90°,且EF交正方形外角∠DCG的平分线CF于点F,求证:AE=EF.
经过思考,小明展示了一种正确的解题思路:在AB上截取BM=BE,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF.
在此基础上,同学们作了进一步的研究:
(1)小颖提出:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(2)小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立。你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
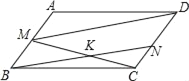
【题目】在ABCD中,AB=1,BC=2,∠B=45°,M为AB的中点.
(1)求tan∠CMD的值;
(2)设N为CD中点,CM交BN于K,求![]() 及S△BKC的值.
及S△BKC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国的农作物主要以水稻、玉米和小麦为主,种植太单调不利于土壤环境的维护,而且对农业的发展也没有促进作用,为了鼓励大豆的种植,国家对种植大豆的农民给予补贴,调动农民种植大豆的积极性.我市乃大豆之乡,今年很多合作社调整种植结构,把种植玉米改成种植大豆,今年我市某合作社共收获大豆200吨,计划采用批发和零售两种方式销售.经市场调查,批发平均每天售出14吨,由于今年我市小型大豆深加工企业的增多,预计能提前完成销售任务,在平均每天批发量不变的情况下,实际平均每天的零售量比原计划的2倍还多14吨,结果提前5天完成销售任务。那么原计划零售平均每天售出多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市对城区部分路段的人行道地砖、绿化带、排水管等公用设施进行全面更新改造,根据市政建设的需要,需在35天内完成工程.现有甲、乙两个工程队有意承包这项工程,经调查知道,乙工程队单独完成此项工程的时间是甲工程队单独完成此项工程时间的2倍,若甲、乙两工程队合作,只需10天完成.
(1)甲、乙两个工程队单独完成此项工程各需多少天?
(2)若甲工程队每天的工程费用是4万元,乙工程队每天的工程费用是2.5万元,请你设计一种方案,既能按时完工,又能使工程费用最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,AB=CB,F为AB延长线上一点,点E在BC上,且AE=CF,若∠CAE=32°,则∠ACF的度数为__________°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:把形如![]() 的二次三项式(或其一部分)配成完全平方式的方法叫配方法.配方法的基本形式是完全平方公式的逆写,即
的二次三项式(或其一部分)配成完全平方式的方法叫配方法.配方法的基本形式是完全平方公式的逆写,即![]() .请根据阅读材料解决下列问题:
.请根据阅读材料解决下列问题:
(1)填空:分解因式![]() _____;
_____;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若![]() 、
、![]() 、
、![]() 分别是
分别是![]() 的三边,且
的三边,且![]() ,试判断
,试判断![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:对于一些次数较高或者是比较复杂的式子进行因式分解时,换元法是一种常用的方法,下面是某同学用换元法对多项式![]() 进行因式分解的过程.
进行因式分解的过程.
解:设![]()
原式![]() (第一步)
(第一步)
![]() (第二步)
(第二步)
![]() (第三步)
(第三步)
![]() (第四步)
(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的__________(填代号).
A.提取公因式 B.平方差公式
C.两数和的完全平方公式 D.两数差的完全平方公式
(2)按照“因式分解,必须进行到每一个多项式因式都不能再分解为止”的要求,该多项式分解因式的最后结果为______________.
(3)请你模仿以上方法对多项式![]() 进行因式分解.
进行因式分解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com