
【题目】某市对城区部分路段的人行道地砖、绿化带、排水管等公用设施进行全面更新改造,根据市政建设的需要,需在35天内完成工程.现有甲、乙两个工程队有意承包这项工程,经调查知道,乙工程队单独完成此项工程的时间是甲工程队单独完成此项工程时间的2倍,若甲、乙两工程队合作,只需10天完成.
(1)甲、乙两个工程队单独完成此项工程各需多少天?
(2)若甲工程队每天的工程费用是4万元,乙工程队每天的工程费用是2.5万元,请你设计一种方案,既能按时完工,又能使工程费用最少.
【答案】(1)甲工程队单独完成该工程需15天,则乙工程队单独完成该工程需30天;(2)应该选择甲工程队承包该项工程.
【解析】
(1)设甲工程队单独完成该工程需x天,则乙工程队单独完成该工程需2x天.再根据“甲、乙两队合作完成工程需要10天”,列出方程解决问题;
(2)首先根据(1)中的结果,从而可知符合要求的施工方案有三种:方案一:由甲工程队单独完成;方案二:由乙工程队单独完成;方案三:由甲乙两队合作完成.针对每一种情况,分别计算出所需的工程费用.
(1)设甲工程队单独完成该工程需![]() 天,则乙工程队单独完成该工程需
天,则乙工程队单独完成该工程需![]() 天.
天.
根据题意得:![]()
方程两边同乘以![]() ,得
,得![]()
解得:![]()
经检验,![]() 是原方程的解.
是原方程的解.
∴当![]() 时,
时,![]() .
.
答:甲工程队单独完成该工程需15天,则乙工程队单独完成该工程需30天.
(2)因为甲乙两工程队均能在规定的35天内单独完成,所以有如下三种方案:
方案一:由甲工程队单独完成.所需费用为:![]() (万元);
(万元);
方案二:由乙工程队单独完成.所需费用为:![]() (万元);
(万元);
方案三:由甲乙两队合作完成.所需费用为:![]() (万元).
(万元).
∵![]() ∴应该选择甲工程队承包该项工程.
∴应该选择甲工程队承包该项工程.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
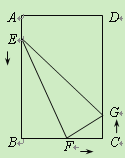
【题目】(12分)如图,在矩形ABCD中,AB=12cm,BC=8cm.点E、F、G分别从点
A、B、C同时出发,沿矩形的边按逆时针方向移动,点E、G的速度均为2cm/s,点F的速
度为4cm/s,当点F追上点G(即点F与点G重合)时,三个点随之停止移动.设移动开始后
第ts时,△EFG的面积为Scm2.
(1)当t=1s时,S的值是多少?
(2)写出S与t之间的函数解析式,并指出自变量t的取值范围;
(3)若点F在矩形的边BC上移动,当t为何值时,以点B、E、F为顶点的三角形与以C、F、G为顶点的三角形相似?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
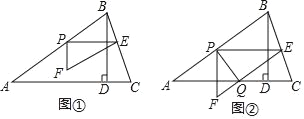
【题目】如图①,在锐角△ABC中,AB=5,tanC=3,BD⊥AC于点D,BD=3,点P从点A出发,以每秒1个单位长度的速度沿AB向终点B运动,过点P作PE∥AC交边BC于点E,以PE为边作Rt△PEF,使∠EPF=90°,点F在点P的下方,且EF∥AB.设△PEF与△ABD重叠部分图形的面积为S(平方单位)(S>0),点P的运动时间为t(秒)(t>0).
(1)求线段AC的长.
(2)当△PEF与△ABD重叠部分图形为四边形时,求S与t之间的函数关系式.
(3)若边EF与边AC交于点Q,连结PQ,如图②.
①当PQ将△PEF的面积分成1:2两部分时,求AP的长.
②直接写出PQ的垂直平分线经过△ABC的顶点时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作![]() ,交射线OB于点D,连接CD;
,交射线OB于点D,连接CD;
(2)分别以点C,D为圆心,CD长为半径作弧,交![]() 于点M,N;
于点M,N;
(3)连接OM,MN.
根据以上作图过程及所作图形,下列结论中错误的是( )

A. ∠COM=∠CODB. 若OM=MN,则∠AOB=20°
C. MN∥CDD. MN=3CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某共享单车公司提供了手机和会员卡两种支付方式.若用手机支付方式,骑行时间在半小时以内(含半小时)不收费,超出半小时后每半小时收费1元,若选择会员卡支付,骑行时间每半小时收费0.8元,设骑行时间为x小时.
(1)根据题意,填写下表(单位:元):
骑行时间(小时) | 0.5 | 2 | 3 | … |
手机支付付款金额(元) | 0 | … | ||
会员卡支付付款金额(元) | 3.2 | … |
(2)设用手机支付付款金额为y1元,用会员卡支付付款金额为y2元,分别写出y1,y2关于x的函数关系式;
(3)若李老师经常骑行该公司的共享单车,他应选择哪种支付方式比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
某校八年级(一)班和(二)班的同学,在双休日参加修整花卉的实践活动.已知(一)班比(二)班每小时多修整2盆花,(一)班修整66盆花所用的时间与(二)班修整60盆花所用时间相等.(一)班和(二)班的同学每小时各修整多少盆花?
查看答案和解析>>
科目:初中数学 来源: 题型:
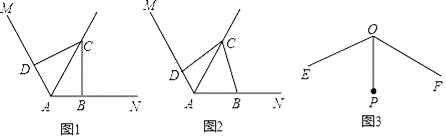
【题目】已知∠MAN=120°,点C是∠MAN的平分线AQ上的一个定点,点B,D分别在AN,AM上,连接BD.
【发现】
(1)如图1,若∠ABC=∠ADC=90°,则∠BCD= °,△CBD是 三角形;
【探索】
(2)如图2,若∠ABC+∠ADC=180°,请判断△CBD的形状,并证明你的结论;
【应用】
(3)如图3,已知∠EOF=120°,OP平分∠EOF,且OP=1,若点G,H分别在射线OE,OF上,且△PGH为等边三角形,则满足上述条件的△PGH的个数一共有 .(只填序号)
①2个②3个③4个④4个以上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等边三角形△ABC,直线1过点C且垂直AC.
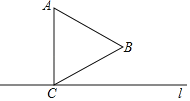
(1)请在直线1上作出点D,使得△ABD的周长最小.
(2)在(1)的条件下,连接AD,BD,求证,AD=2BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】进价为每件40元的某商品,售价为每件50元时,每星期可卖出500件,市场调查反映:如果每件的售价每降价1元,每星期可多卖出100件,但售价不能低于每件42元,且每星期至少要销售800件.设每件降价x元 (x为正整数),每星期的利润为y元.
(1)求y与x的函数关系式并写出自变量x的取值范围;
(2)若某星期的利润为5600元,此利润是否是该星期的最大利润?说明理由.
(3)直接写出售价为多少时,每星期的利润不低于5000元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com