
【题目】(12分)如图,在矩形ABCD中,AB=12cm,BC=8cm.点E、F、G分别从点
A、B、C同时出发,沿矩形的边按逆时针方向移动,点E、G的速度均为2cm/s,点F的速
度为4cm/s,当点F追上点G(即点F与点G重合)时,三个点随之停止移动.设移动开始后
第ts时,△EFG的面积为Scm2.
(1)当t=1s时,S的值是多少?
(2)写出S与t之间的函数解析式,并指出自变量t的取值范围;
(3)若点F在矩形的边BC上移动,当t为何值时,以点B、E、F为顶点的三角形与以C、F、G为顶点的三角形相似?请说明理由。
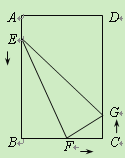
【答案】解:(1)如图(甲),当![]() 秒时,AE=2,EB=10,BF=4,FC=4,CG=2
秒时,AE=2,EB=10,BF=4,FC=4,CG=2
由![]()
=![]()
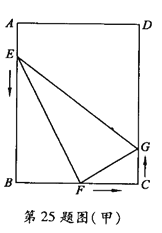
(2)①如图(甲),当![]() 时,点E、F、G分别在边AB、BC、CD上移动,
时,点E、F、G分别在边AB、BC、CD上移动,
此时![]()
![]()
![]()
即![]() (
(![]() )
)
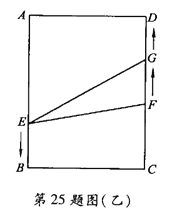
②如图(乙)当点F追上点G时,![]() ,解得
,解得![]() .
.
当![]() 时,点E在边AB上移动,点F、G都在边CD上移动.
时,点E在边AB上移动,点F、G都在边CD上移动.
此时CF=![]() .CG=
.CG=![]() .
.
FG=CG-CF=![]()
![]()
即![]() (
(![]() )
)
(3)如图(甲),当点F在矩形的边BC上移动时,![]() .
.
在△EBF和△FCG中,∠B=∠C=90°.
①若![]() .即
.即![]() ,解得
,解得![]() 。
。
又![]() 满足
满足![]() ,所以当
,所以当![]() 时,△EBF∽△FCG.
时,△EBF∽△FCG.
②若![]() .即
.即![]() ,解得
,解得![]() 。
。
又![]() 满足
满足![]() ,所以当
,所以当![]() 时,△EBF∽△GCF.
时,△EBF∽△GCF.
综上所述,当![]() 或
或![]() 时,以点E、B、F为顶点的三角形与以F、C、G为顶点的三角形相似.
时,以点E、B、F为顶点的三角形与以F、C、G为顶点的三角形相似.
【解析】略


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
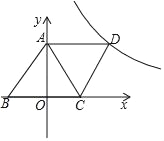
【题目】如图,在平面直角坐标系中,四边形ABCD是菱形,点A(0,4),B(﹣3,0)反比例函数y=![]() (k为常数,k≠0,x>0)的图象经过点D.
(k为常数,k≠0,x>0)的图象经过点D.
(1)填空:k=_____.
(2)已知在y=![]() 的图象上有一点N,y轴上有一点M,且四边形ABMN是平行四边形,求点M的坐标.
的图象上有一点N,y轴上有一点M,且四边形ABMN是平行四边形,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,过点F(0,1)的直线y=kx+b与抛物线![]() 交于M(x1,y1)和N(x2,y2)两点(其中x1<0,x2<0).
交于M(x1,y1)和N(x2,y2)两点(其中x1<0,x2<0).
⑴求b的值.
⑵求x1x2的值
⑶分别过M、N作直线l:y=-1的垂线,垂足分别是M1、N1,判断△M1FN1的形状,并证明你的结论.
⑷对于过点F的任意直线MN,是否存在一条定直线m,使m与以MN为直径的圆相切.如果有,请法度出这条直线m的解析式;如果没有,请说明理由.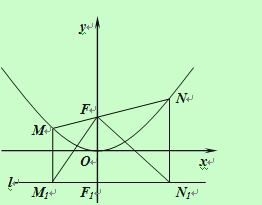
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是圆
是圆![]() 的直径,
的直径,![]() ,点
,点![]() 是圆
是圆![]() 上一动点(与
上一动点(与![]() ,
,![]() 不重合),
不重合),![]() 的平分线交圆
的平分线交圆![]() 于
于![]() .
.
![]() 判断
判断![]() 的形状,并证明你的结论;
的形状,并证明你的结论;
![]() 若
若![]() 是
是![]() 的内心,当点
的内心,当点![]() 运动时,
运动时,![]() 、
、![]() 中是否存在长度保持不变的线段?如果存在,请指出并求其长度;如果不存在,请说明理由.
中是否存在长度保持不变的线段?如果存在,请指出并求其长度;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,A(-1,0)、B(0,-2),顶点C、D在双曲线![]() (x>0)上,边AD交y轴于点E,若点E恰好是AD的中点,则k=_____.
(x>0)上,边AD交y轴于点E,若点E恰好是AD的中点,则k=_____.
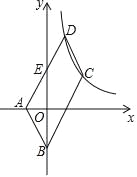
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市对城区部分路段的人行道地砖、绿化带、排水管等公用设施进行全面更新改造,根据市政建设的需要,需在35天内完成工程.现有甲、乙两个工程队有意承包这项工程,经调查知道,乙工程队单独完成此项工程的时间是甲工程队单独完成此项工程时间的2倍,若甲、乙两工程队合作,只需10天完成.
(1)甲、乙两个工程队单独完成此项工程各需多少天?
(2)若甲工程队每天的工程费用是4万元,乙工程队每天的工程费用是2.5万元,请你设计一种方案,既能按时完工,又能使工程费用最少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com