
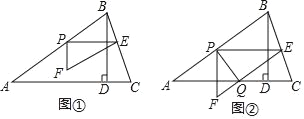
【题目】如图①,在锐角△ABC中,AB=5,tanC=3,BD⊥AC于点D,BD=3,点P从点A出发,以每秒1个单位长度的速度沿AB向终点B运动,过点P作PE∥AC交边BC于点E,以PE为边作Rt△PEF,使∠EPF=90°,点F在点P的下方,且EF∥AB.设△PEF与△ABD重叠部分图形的面积为S(平方单位)(S>0),点P的运动时间为t(秒)(t>0).
(1)求线段AC的长.
(2)当△PEF与△ABD重叠部分图形为四边形时,求S与t之间的函数关系式.
(3)若边EF与边AC交于点Q,连结PQ,如图②.
①当PQ将△PEF的面积分成1:2两部分时,求AP的长.
②直接写出PQ的垂直平分线经过△ABC的顶点时t的值.
【答案】(1)5;(2)当0<t≤1时,S=![]() t2+
t2+![]() t;当
t;当![]() ≤t<5时,S=
≤t<5时,S=![]() (5﹣t)2;(3)①
(5﹣t)2;(3)①![]() 或
或![]() ;②
;②![]() 或
或![]() .
.
.
【解析】试题分析:
(1)在Rt△ABD中,由∠BDA=90°,AB=5,BD=3,可由勾股定理求得AD=4;在Rt△BCD中,∠BDC=90°,BD=3,tanc=3,可求得CD=1;由此可得AC=AD+CD=5;
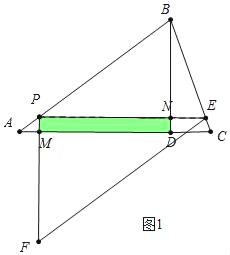
(2)由题意分析可知,如图1,当点D在线段EF上或EF的下方时,△PEF与△ABD重叠部分图形为矩形PMDN;如图2,当点F落到AC上或AC的上方时,△PEF与△ABD重叠部分图形为四边形PMFN;分这两种情况分析讨论即可;
(3)①如图3、图4,分I、S△PFQ:S△PEQ=1:2和II、 S△PFQ:S△PEQ=2:1两种情况讨论,由此可分别可得到:S△PEQ:S△PEF=2:3和S△PEQ:S△PEF=1:3从而可得:PG:PF=2:3和PG:PF=1:3,结合PG= ![]() ,PF=
,PF=![]() 即可解得所求AP的长;
即可解得所求AP的长;
②如图5、图6,分I、PQ的垂直平分线经过当点A和II、PQ的垂直平分线经过点B两种情况分析讨论即可求得对应的t的值.
试题解析:
(1)在Rt△ABD中,∠BDA=90°,AB=5,BD=3,
∴AD=![]() ,
,
在Rt△BCD中,∠BDC=90°,BD=3,tanc=3,
∴CD=![]() ,
,
∴AC=AD+CD=4+1=5.
(2)如图1中,当0<t≤1时,重叠部分是四边形PMDN.
易知PA=t,AM=![]() t,PM=
t,PM=![]() t,DM=4﹣
t,DM=4﹣![]() t,
t,
∴S=![]() t(4﹣
t(4﹣![]() t)=﹣
t)=﹣![]() t2+
t2+![]() t.
t.
如图2中,当![]() ≤t<5时,重叠部分是四边形PNMF.
≤t<5时,重叠部分是四边形PNMF.

∵AB=5,AC=AD+CD=4+1=5,
∴AC=AB,
易证PB=PE=5﹣t,PF=![]() (5﹣t),PN=
(5﹣t),PN=![]() (5﹣t),
(5﹣t),
S=![]() (5﹣t)
(5﹣t)![]() (5﹣t)﹣
(5﹣t)﹣![]() (5﹣t)
(5﹣t)![]() (5﹣t)=
(5﹣t)=![]() (5﹣t)2.
(5﹣t)2.
(3)①如图3中,PF交AC于G.
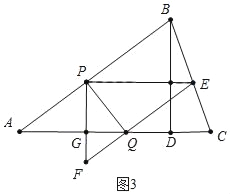
当S△PFQ:S△PEQ=1:2时,
∴S△PEQ:S△PEF=2:3,
∴![]() PEPG:
PEPG: ![]() PEPF=2:3,
PEPF=2:3,
∴PG:PF=2:3,
∴![]() t:
t: ![]() (5﹣t)=2:3.
(5﹣t)=2:3.
∴t=![]() ,即AP=
,即AP=![]() .
.
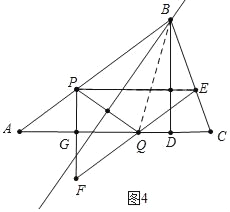
如图4中,当S△PFQ:S△PEQ=2:1时,
∴S△PEQ:S△PEF=1:3,
∴![]() PEPG:
PEPG: ![]() PEPF=1:3,
PEPF=1:3,
∴PG:PF=1:3,
∴![]() t:
t: ![]() (5﹣t)=1:3.
(5﹣t)=1:3.
∴t=![]() ,即AP=
,即AP=![]() ,
,
∴AP的值为![]() 或
或![]() .
.
②如图5中,当PQ的垂直平分线经过当A时.
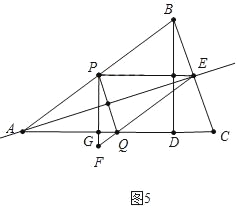
易知四边形APEQ时菱形,
∴PE=PA,即t=5﹣t,
∴t=![]() .
.
如图6中,当PQ的垂直平分线经过点B时,作EN⊥AC于N,EP交BD于M.
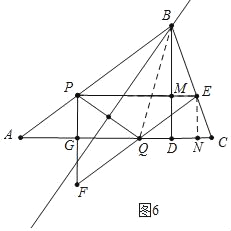
易知四边形PENG时矩形,四边形DMEN时矩形,
∴PG=EN=![]() t,EM=DN=PE﹣PM=
t,EM=DN=PE﹣PM=![]() (5﹣t),
(5﹣t),
QN=![]() EN=
EN=![]() t,
t,
∴QD=![]() t﹣
t﹣![]() (5﹣t)=t﹣1,
(5﹣t)=t﹣1,
在Rt△BQD中,∵BQ2=QD2+BD2,
∴(5﹣t)2=32+(t﹣1)2,
∴t=![]() .
.
综上所述,t=![]() s或
s或![]() s时,PQ的垂直平分线过△ABC的顶点.
s时,PQ的垂直平分线过△ABC的顶点.


 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】共享经济来临,某企业决定在无锡投入共享单车(自行车)和共享电单车(电动车)共2000辆,已知每辆共享单车成本380元,每台共享电单车成本1500元,2辆共享单车和1辆共享电单车每周毛利31元,4辆共享单车和3辆共享电单车每周毛利81元,
(1)求共享单车和共享电单车每周每辆分别可以盈利多少元?
(2)为考虑投资回报率,该企业计划投入成本不超过174万元,每周的毛利不低于23050元,现要求投入的单车数量为10的倍数,请你列举出所有投入资金方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:一般地,![]() 个相同的因数
个相同的因数![]() 相乘
相乘 ![]() ,记为
,记为![]() .如
.如![]() ,此时,
,此时,![]() 叫做以
叫做以![]() 为底
为底![]() 的对数,记为
的对数,记为![]() (即
(即![]() ).一般地,若
).一般地,若![]() ,(
,(![]() 且
且![]() ,
,![]() ),则
),则![]() 叫做以
叫做以![]() 为底
为底![]() 的对数,记为
的对数,记为![]() (即
(即![]() ).如
).如![]() ,则
,则![]() 叫做以
叫做以![]() 为底
为底![]() 的对数,记为
的对数,记为![]() (即
(即![]() ).
).
(1)计算以下各对数的值:![]() __________,
__________,![]() __________,
__________,![]() __________.
__________.
(2)观察(1)中三数![]() 、
、![]() ,
,![]() 之间满足怎样的关系式,
之间满足怎样的关系式,![]() 、
、![]() 、
、![]() 之间又满足怎样的关系式;
之间又满足怎样的关系式;
(3)由(2)的结果,你能归纳出一个一般性的结论吗?![]() __________.(
__________.(![]() 且
且![]() ,
,![]() ,
,![]() )
)
(4)根据幂的运算法则:![]() 以及对数的含义证明上述结论.
以及对数的含义证明上述结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AD=4,对角线AC与BD交于点O,OE⊥AC交BC于点E,CE=3,则矩形ABCD的面积为( )
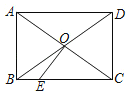
A.![]() B.
B.![]() C.12D.32
C.12D.32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线![]() 与⊙O,AB是⊙O的直径,AD⊥
与⊙O,AB是⊙O的直径,AD⊥![]() 于点D.
于点D.
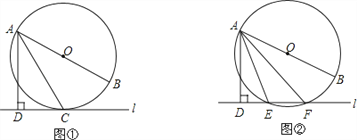
(1)如图①,当直线![]() 与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;
与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;
(2)如图②,当直线![]() 与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小.
与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)与x轴交于不同的两个点A(x1,0)和点B(x2,0)与y轴的正半轴交于点C,如果x1,x2是方程x2﹣2x﹣3=0的两个根(x1<x2),且图象经过点(2,3)
(1)求抛物线的解析式并画出图象
(2)x在什么范围内函数值y大于3且随x的增大而增大.
(3)设(1)中的抛物线顶点为D,在y轴上是否存在点P,使得DP+BP的和最小?若存在,求出这个最小值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与坐标轴分别交于A(﹣2,0),B(0,1)两点,与反比例函数的图象在第一象限交于点C(4,n),求一次函数和反比例函数的解析式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com