
【题目】等边三角形△ABC,直线1过点C且垂直AC.
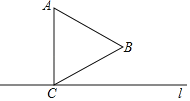
(1)请在直线1上作出点D,使得△ABD的周长最小.
(2)在(1)的条件下,连接AD,BD,求证,AD=2BD.
科目:初中数学 来源: 题型:
【题目】某市对城区部分路段的人行道地砖、绿化带、排水管等公用设施进行全面更新改造,根据市政建设的需要,需在35天内完成工程.现有甲、乙两个工程队有意承包这项工程,经调查知道,乙工程队单独完成此项工程的时间是甲工程队单独完成此项工程时间的2倍,若甲、乙两工程队合作,只需10天完成.
(1)甲、乙两个工程队单独完成此项工程各需多少天?
(2)若甲工程队每天的工程费用是4万元,乙工程队每天的工程费用是2.5万元,请你设计一种方案,既能按时完工,又能使工程费用最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温度与我们的生活息息相关,如图是一个温度计实物示意图,左边的刻度是摄氏温度(℃),右边的刻度是华氏温度(℉).设摄氏温度为x(℃)华氏温度为y(℉),则y是x的一次函数,通过观察我们发现,温度计上的摄氏温度为0℃时,华氏温度为32℉;摄氏温度为﹣20℃时,华氏温度为﹣4℉

请根据以上信息,解答下列问题
(1)仔细观察图中数据,试求出y与x的函数关系式;
(2)当摄氏温度为﹣5℃时,华氏温度为多少?
(3)当华氏温度为59℉时,摄氏温度为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,在AC边上取两点M、N,使∠MBN=30°.若AM=m,MN=x,CN=n,则以x,m,n为边长的三角形的形状为( )
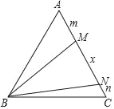
A. 锐角三角形 B. 直角三角形
C. 钝角三角形 D. 随x,m,n的值而定
查看答案和解析>>
科目:初中数学 来源: 题型:
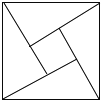
【题目】如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为![]() ,较短直角边长为
,较短直角边长为![]() ,若
,若![]() ,大正方形的面积为13,则小正方形的面积为________.
,大正方形的面积为13,则小正方形的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】精准扶贫,助力苹果产业大发展.甲、乙两超市为响应党中央将消除贫困和实现共同富裕作为重要的奋斗目标,到种植苹果的贫困山区分别用![]() 元以相同的进价购进质量相同的苹果.甲超市的销售方案:将苹果按大小分类包装销售,其中大苹果
元以相同的进价购进质量相同的苹果.甲超市的销售方案:将苹果按大小分类包装销售,其中大苹果![]() 千克,以进价的
千克,以进价的![]() 倍价格销售,剩下的小苹果以高于进价的
倍价格销售,剩下的小苹果以高于进价的![]() 销售.乙超市的销售方案:不将苹果按大小分类,直接包装销售,价格按甲超市大、小两种苹果售价的平均数定价.若两超市将苹果全部售完,其中甲超市获利
销售.乙超市的销售方案:不将苹果按大小分类,直接包装销售,价格按甲超市大、小两种苹果售价的平均数定价.若两超市将苹果全部售完,其中甲超市获利![]() 元(包含人工工资和运费).
元(包含人工工资和运费).
(1)苹果进价为每千克多少元?
(2)乙超市获利多少元?并比较哪种销售方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个分式的分子或分母可以因式分解,且这个分式不可约分,那么我们称这
个分式为“和谐分式”.
(1)下列分式:①![]() ;②
;②![]() ;③
;③![]() ;④
;④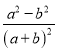 . 其中是“和谐分式”是 (填写序号即可);
. 其中是“和谐分式”是 (填写序号即可);
(2)若![]() 为正整数,且
为正整数,且![]() 为“和谐分式”,请写出
为“和谐分式”,请写出![]() 的值;
的值;
(3)在化简![]() 时,
时,
小东和小强分别进行了如下三步变形:
小东: ![]()
![]()

小强: ![]()
![]()
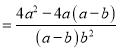
显然,小强利用了其中的和谐分式, 第三步所得结果比小东的结果简单,
原因是: ,
请你接着小强的方法完成化简.
查看答案和解析>>
科目:初中数学 来源: 题型:
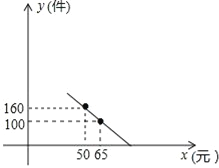
【题目】某商场老板对一种新上市商品的销售情况进行记录,已知这种商品进价为每件40元,经过记录分析发现,当销售单价在40元至90元之间(含40元和90元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数,其图象如图所示.
(1)求y与x的函数关系式.
(2)设商场老板每月获得的利润为P(元),求P与x之间的函数关系式;
(3)如果想要每月获得2400元的利润,那么销售单价应定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com