
����Ŀ������ƶ������ƻ����ҵ��չ���ס���������Ϊ��Ӧ�����뽫����ƶ����ʵ�ֹ�ͬ��ԣ��Ϊ��Ҫ�ķܶ�Ŀ�꣬����ֲƻ����ƶ��ɽ���ֱ���![]() Ԫ����ͬ�Ľ��۹���������ͬ��ƻ�����׳��е����۷�������ƻ������С�����װ���ۣ����д�ƻ��
Ԫ����ͬ�Ľ��۹���������ͬ��ƻ�����׳��е����۷�������ƻ������С�����װ���ۣ����д�ƻ��![]() ǧ�ˣ��Խ��۵�
ǧ�ˣ��Խ��۵�![]() ���۸����ۣ�ʣ�µ�Сƻ���Ը��ڽ��۵�
���۸����ۣ�ʣ�µ�Сƻ���Ը��ڽ��۵�![]() ���ۣ��ҳ��е����۷���������ƻ������С���ֱ࣬�Ӱ�װ���ۣ��۸׳��д�С����ƻ���ۼ۵�ƽ�������ۣ��������н�ƻ��ȫ�����꣬���м׳��л���
���ۣ��ҳ��е����۷���������ƻ������С���ֱ࣬�Ӱ�װ���ۣ��۸׳��д�С����ƻ���ۼ۵�ƽ�������ۣ��������н�ƻ��ȫ�����꣬���м׳��л���![]() Ԫ�������˹����ʺ��˷ѣ���
Ԫ�������˹����ʺ��˷ѣ���
��1��ƻ������Ϊÿǧ�˶���Ԫ��
��2���ҳ��л�������Ԫ�����Ƚ��������۷�ʽ�����㣮
���𰸡���1��10��2��165000����ƻ������С�����װ���۸����㣮
��������
��1������ƻ������Ϊÿǧ��xԪ�����������н�ƻ��ȫ�����꣬���м׳��л���210000Ԫ�г����̣����x��ֵ���ٽ��м��鼴������𰸣�
��2�����ݣ�1�����ÿ������ƻ���������ٸ��ݴ�Сƻ���ۼ۷ֱ�Ϊ10Ԫ��5.5Ԫ������ҳ��л���������׳��л���210000Ԫ��Ƚϼ��ɣ�
��1����ƻ������Ϊÿǧ��xԪ����������ã�
![]() ��2x����1��10%��x��
��2x����1��10%��x��![]() 20000��300000��210000��
20000��300000��210000��
��ã�x��10��
������x��10��ԭ���̵Ľ⣬
��ƻ������Ϊÿǧ��10Ԫ��
��2���ɣ�1���ã�ÿ������ƻ������Ϊ��![]() ��30000��ǧ�ˣ���
��30000��ǧ�ˣ���
��Сƻ���ۼ۷ֱ�Ϊ20Ԫ��11Ԫ��
���ҳ��л���30000����![]() 10����165000��Ԫ����
10����165000��Ԫ����
�׳��л���210000Ԫ��
��210000��165000��
�ཫƻ������С�����װ���ۣ������㣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
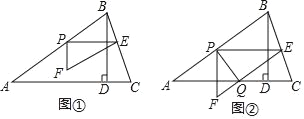
����Ŀ����ͼ�٣��������ABC�У�AB=5��tanC=3��BD��AC�ڵ�D��BD=3����P�ӵ�A��������ÿ��1����λ���ȵ��ٶ���AB���յ�B�˶�������P��PE��AC����BC�ڵ�E����PEΪ����Rt��PEF��ʹ��EPF=90������F�ڵ�P���·�����EF��AB������PEF����ABD�ص�����ͼ�ε����ΪS��ƽ����λ����S��0������P���˶�ʱ��Ϊt���룩��t��0����
��1�����߶�AC�ij���
��2������PEF����ABD�ص�����ͼ��Ϊ�ı���ʱ����S��t֮��ĺ�����ϵʽ��
��3������EF���AC���ڵ�Q������PQ����ͼ����
�ٵ�PQ����PEF������ֳ�1��2������ʱ����AP�ij���
��ֱ��д��PQ�Ĵ�ֱƽ���߾�����ABC�Ķ���ʱt��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
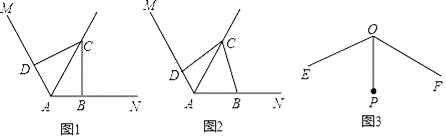
����Ŀ����֪��MAN=120������C�ǡ�MAN��ƽ����AQ�ϵ�һ�����㣬��B��D�ֱ���AN��AM�ϣ�����BD��
�����֡�
��1����ͼ1������ABC=��ADC=90�������BCD=�� ��������CBD���� �������Σ�
��̽����
��2����ͼ2������ABC+��ADC=180�������ж���CBD����״����֤����Ľ��ۣ�
��Ӧ�á�
��3����ͼ3����֪��EOF=120����OPƽ�֡�EOF����OP=1������G��H�ֱ�������OE��OF�ϣ�����PGHΪ�ȱ������Σ�������������������PGH�ĸ���һ������ ������ֻ����ţ�
��2����3����4����4������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ȱ���������ABC��ֱ��1����C�Ҵ�ֱAC��
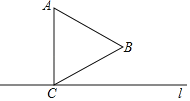
��1������ֱ��1��������D��ʹ����ABD���ܳ���С��
��2���ڣ�1���������£�����AD��BD����֤��AD��2BD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾Ϊһ�����͵��Ӳ�Ʒ�ڸó��е���Լ�����̣���֪ÿ����Ʒ�Ľ���Ϊ40Ԫ���ù�˾ÿ���������ֲ�Ʒ��������֧�����������ۣ��ܼ�100��Ԫ�������۹����е�֪����������y������������۵���x��Ԫ��֮����������ʾ�ĺ�����ϵ�����ҷ���y��x��һ�κ�����
���۵���x��Ԫ�� | 50 | 60 | 70 | 80 |
��������y������� | 5.5 | 5 | 4.5 | 4 |
��1����y��x�ĺ�����ϵʽ��
��2���ʣ������۵���xΪ��ֵʱ���ù�˾������������������ֵ��
����ע��������=�����۶�ܽ����۩�������֧��
��3������˾ϣ����������60��Ԫ����������ù�˾ȷ�����۵��۵ķ�Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ţ�3����Ϊ����Ӳμ�ѧУ���е�����ˮ������֪ʶ�������ڰ���ѡȡ��������ѧ�����ֳ�������ͬ�ļס������飬�������Ĵ�����ˮ������ģ�⾺�����ɼ�����������������ʷֱ���Ƴ���ͼͳ��ͼ��
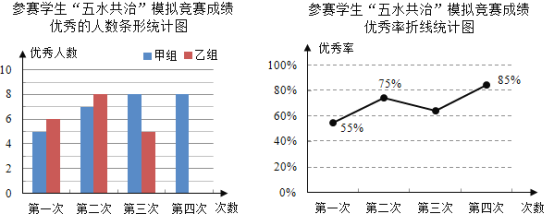
����ͳ��ͼ������������⣺
��1�������γɼ����������Ƕ��٣���������ͳ��ͼ����������
��2������ü���ɼ�����������ƽ����![]() ������
������![]() ����ͨ������˵������һ��ɼ�����������Ƚ��ȶ���
����ͨ������˵������һ��ɼ�����������Ƚ��ȶ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
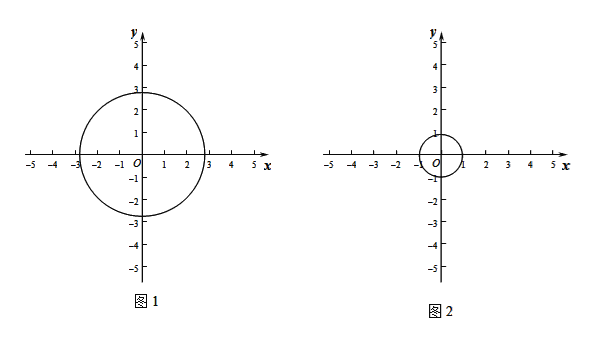
����Ŀ����ƽ��ֱ������ϵ�У������P��x��y���ı任��ΪP�䣨x+y��x��y����
��1����ͼ1�������O�İ뾶Ϊ2![]() ��
��
���ж�M��2��0����N����2��1��������ı任��M�䡢N�����O��λ�ù�ϵ��
������P��ֱ��y=x-2�ϣ���P�ı任��P�����ڡ�O�⣬���ͼ�����P������x��ȡֵ��Χ��
��2����ͼ2�������O�İ뾶Ϊ1����P�ı任��P����ֱ��y=��2x+5�ϣ����P���O������һ��������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ϊÿ��40Ԫ��ij��Ʒ���ۼ�Ϊÿ��50Ԫʱ��ÿ���ڿ�����500�����г����鷴ӳ�����ÿ�����ۼ�ÿ����1Ԫ��ÿ���ڿɶ�����100�������ۼ۲��ܵ���ÿ��42Ԫ����ÿ��������Ҫ����800������ÿ������xԪ ��xΪ����������ÿ���ڵ�����ΪyԪ��
��1����y��x�ĺ�����ϵʽ��д���Ա���x��ȡֵ��Χ��
��2����ij���ڵ�����Ϊ5600Ԫ���������Ƿ��Ǹ����ڵ��������˵�����ɣ�
��3��ֱ��д���ۼ�Ϊ����ʱ��ÿ���ڵ�������5000Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������⣩
��![]() ��
��![]() ��
��![]() ����
����![]() ��ֱ��
��ֱ��![]() �ϣ�
�ϣ�![]() ���⣩���ֱ���
���⣩���ֱ���![]() �͵�
�͵�![]() ��
��![]() ��
��![]() �Ĵ��ߣ��������߽��ڵ�
�Ĵ��ߣ��������߽��ڵ�![]() ���о�
���о�![]() ��
��![]() ��������ϵ.
��������ϵ.
��̽�����֣�
ij��ѧ��ȤС����̽��![]() ��
��![]() �Ĺ�ϵʱ�������������һ��������ѧ˼�룬���Ƿ��ֵ���
�Ĺ�ϵʱ�������������һ��������ѧ˼�룬���Ƿ��ֵ���![]() ��
��![]() �е�ʱ��ֻ��Ҫȡ
�е�ʱ��ֻ��Ҫȡ![]() �ߵ��е�
�ߵ��е�![]() ����ͼ1����ͨ������֤���Ϳ��Եõ�
����ͼ1����ͨ������֤���Ϳ��Եõ�![]() ��
��![]() ��������ϵ�����㰴������˼·ֱ��д��
��������ϵ�����㰴������˼·ֱ��д��![]() ��
��![]() ��������ϵ��
��������ϵ��
����ѧ˼����
��ô��![]() ��ֱ��
��ֱ��![]() �ϣ�
�ϣ�![]() ���⣩�������������䣩������õ��Ľ����Ƿ���Ȼ�����أ�
���⣩�������������䣩������õ��Ľ����Ƿ���Ȼ�����أ�
���������![]() ���߶�
���߶�![]() ��������
��������![]() ���߶�
���߶�![]() ���ӳ�����������
���ӳ�����������![]() ���߶�
���߶�![]() �ķ����ӳ���������������У���ѡһ���������ͼ2�л���ͼ�Σ���֤����Ľ���.
�ķ����ӳ���������������У���ѡһ���������ͼ2�л���ͼ�Σ���֤����Ľ���.
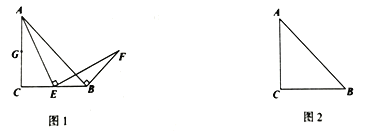
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com