
【题目】在平面直角坐标系中,定义点P(x,y)的变换点为P′(x+y,x﹣y).
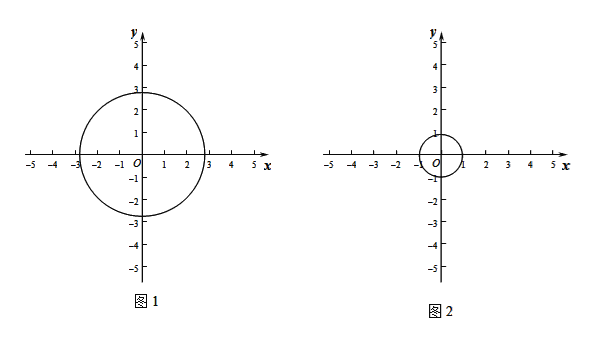
(1)如图1,如果⊙O的半径为2![]() ,
,
①判断M(2,0),N(﹣2,1)两个点的变换点M′、N′与⊙O的位置关系;
②若点P在直线y=x-2上,点P的变换点P′不在⊙O外,结合图形求点P横坐标x的取值范围.
(2)如图2,如果⊙O的半径为1,且P的变换点P′在直线y=﹣2x+5上,求点P与⊙O上任意一点距离的最小值.
【答案】(1)①M’点在圆O上,点N’不在圆O上.;②![]() ;(2)
;(2)![]() .
.
【解析】
(1)①根据新定义得到点M的变换点M′的坐标为(2,2),于是根据勾股定理计算出OM′=2![]() ,则根据点与圆的位置关系的判定方法可判断点M的变换点在⊙O上;同样方法可判断点N(-1,-3)的变换点在⊙O外;②利用一次函数图象上点的坐标特征,设P点坐标为(x,x-2),利用新定义得到P点的变换点为P′的坐标为(2x-2, 2),则根据勾股定理计算出OP′=
,则根据点与圆的位置关系的判定方法可判断点M的变换点在⊙O上;同样方法可判断点N(-1,-3)的变换点在⊙O外;②利用一次函数图象上点的坐标特征,设P点坐标为(x,x-2),利用新定义得到P点的变换点为P′的坐标为(2x-2, 2),则根据勾股定理计算出OP′=![]() ,然后利用点与圆的位置关系得到
,然后利用点与圆的位置关系得到![]() ≤2
≤2![]() ,解不等式得
,解不等式得![]() ;
;
(2)设点P′的坐标为(x,-2x+5),P(m,n),根据新定义得到m+n=x,m-n=-2x+5,消去x得3m+n=5,则n=-3m+5,于是得到P点坐标为(m,-3m+5),则可判断点P在直线y=-3x+5上,设直线y=-3x+5与x轴相交于点A,与y轴相交于点B,过O点作OH⊥AB于H,交⊙O于C,如图2,易得A(![]() ,0),B(0,5),利用勾股定理计算出AB=
,0),B(0,5),利用勾股定理计算出AB=![]() ,再利用面积法计算出OH=
,再利用面积法计算出OH=![]() ,所以CH=
,所以CH=![]() -1,当点P在H点时,PC为点P与⊙O上任意一点距离的最小值.
-1,当点P在H点时,PC为点P与⊙O上任意一点距离的最小值.
(1)①M(2,0)的变换点M′的坐标为(2,2),则OM′=![]() =2
=2![]() ,所以点M(2,0)的变换点在⊙O上;
,所以点M(2,0)的变换点在⊙O上;
N(-2,1)的变换点N′的坐标为(-1,-3),则ON′=![]() =
=![]() >2
>2![]() ,所以点N(-2,-1)的变换点在⊙O外;
,所以点N(-2,-1)的变换点在⊙O外;
②设P点坐标为(x,x-2),则P点的变换点为P′的坐标为(2x-2,2),则OP′=![]() ,
,
∵点P′不在⊙O外,
∴![]() ≤2
≤2![]() ,
,
∴(2x-2)2≤4,即(x-1)2≤1,
∴-1≤x-1≤1,解得0≤x≤2,
即点P横坐标的取值范围为0≤x≤2;
(2)设点P′的坐标为(x,-2x+5),P(m,n),
根据题意得m+n=x,m-n=-2x+5,
∴3m+n=5,
即n=-3m+5,
∴P点坐标为(m,-3m+5),
∴点P在直线y=-3x+5上,
设直线y=-3x+5与x轴相交于点A,与y轴相交于点B,过O点作OH⊥AB于H,交⊙O于C,如图,
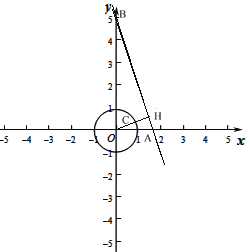
则A(![]() ,0),B(0,5),
,0),B(0,5),
∴AB=![]() =
=![]() ,
,
∵![]() OHAB=
OHAB=![]() OAOB,
OAOB,
∴OH=![]() =
=![]() ,
,
∴CH=![]() -1,
-1,
即点P与⊙O上任意一点距离的最小值为![]() -1.
-1.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点
轴分别相交于点![]() 、点
、点![]() ,
,![]() ,若将
,若将![]() 沿直线
沿直线![]() 折叠,使点
折叠,使点![]() 与点
与点![]() 重合,折痕
重合,折痕![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 交于点
交于点![]() .
.
(1)求![]() 的值;
的值;
(2)求点![]() 的坐标;
的坐标;
(3)求直线![]() 的表达式.
的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
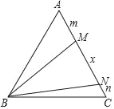
【题目】如图,在等边三角形ABC中,在AC边上取两点M、N,使∠MBN=30°.若AM=m,MN=x,CN=n,则以x,m,n为边长的三角形的形状为( )
A. 锐角三角形 B. 直角三角形
C. 钝角三角形 D. 随x,m,n的值而定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】精准扶贫,助力苹果产业大发展.甲、乙两超市为响应党中央将消除贫困和实现共同富裕作为重要的奋斗目标,到种植苹果的贫困山区分别用![]() 元以相同的进价购进质量相同的苹果.甲超市的销售方案:将苹果按大小分类包装销售,其中大苹果
元以相同的进价购进质量相同的苹果.甲超市的销售方案:将苹果按大小分类包装销售,其中大苹果![]() 千克,以进价的
千克,以进价的![]() 倍价格销售,剩下的小苹果以高于进价的
倍价格销售,剩下的小苹果以高于进价的![]() 销售.乙超市的销售方案:不将苹果按大小分类,直接包装销售,价格按甲超市大、小两种苹果售价的平均数定价.若两超市将苹果全部售完,其中甲超市获利
销售.乙超市的销售方案:不将苹果按大小分类,直接包装销售,价格按甲超市大、小两种苹果售价的平均数定价.若两超市将苹果全部售完,其中甲超市获利![]() 元(包含人工工资和运费).
元(包含人工工资和运费).
(1)苹果进价为每千克多少元?
(2)乙超市获利多少元?并比较哪种销售方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从宁海县到某市,可乘坐普通列车或高铁,已知高铁的行驶路程与普通列车的行驶路程之和是920千米,而普通列车的行驶路程是高铁的行驶路程的1.3倍.
(1)求普通列车的行驶路程;
(2)若高铁的平均速度(千米/时)是普通列车的平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求高铁的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个分式的分子或分母可以因式分解,且这个分式不可约分,那么我们称这
个分式为“和谐分式”.
(1)下列分式:①![]() ;②
;②![]() ;③
;③![]() ;④
;④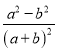 . 其中是“和谐分式”是 (填写序号即可);
. 其中是“和谐分式”是 (填写序号即可);
(2)若![]() 为正整数,且
为正整数,且![]() 为“和谐分式”,请写出
为“和谐分式”,请写出![]() 的值;
的值;
(3)在化简![]() 时,
时,
小东和小强分别进行了如下三步变形:
小东: ![]()
![]()

小强: ![]()
![]()
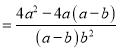
显然,小强利用了其中的和谐分式, 第三步所得结果比小东的结果简单,
原因是: ,
请你接着小强的方法完成化简.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)若△ABC和△A1B1C1关于原点O成中心对称图形,画出△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2;
(3)在x轴上存在一点P,满足点P到点B1与点C1距离之和最小,请直接写出P B1+ P C1的最小值为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
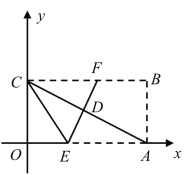
【题目】如图,把长方形纸片![]() 放入平面直角坐标系中,使
放入平面直角坐标系中,使![]() 分别落在
分别落在![]() 轴的的正半轴上,连接
轴的的正半轴上,连接![]() ,且
,且![]() ,
,![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)将纸片![]() 折叠,使点
折叠,使点![]() 与点
与点![]() 重合(折痕为
重合(折痕为![]() ),求折叠后纸片重叠部分
),求折叠后纸片重叠部分![]() 的面积;
的面积;
(3)求![]() 所在直线的函数表达式,并求出对角线
所在直线的函数表达式,并求出对角线![]() 与折痕
与折痕![]() 交点
交点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形ABCD中,E是AB边的中点,DE交AC于点F,AC、DE把它分成的四部分的面积分别为S1S2S3S4,下面结论:
①只有一对相似三角形
②EF:ED=1:2
③S1:S2:S3:S4=1:2:4:5
其中正确的结论是( )
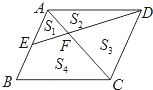
A.①③ B.③ C.① D.①②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com