【题目】某市出租车计费办法如图所示．根据图象信息，下列说法错误的是（ ）
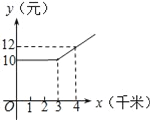
A. 出租车起步价是10元
B. 在3千米内只收起步价
C. 超过3千米部分（x＞3）每千米收3元
D. 超过3千米时（x＞3）所需费用y与x之间的函数关系式是y=2x+4
科目：初中数学 来源： 题型：
【题目】某高校学生会在某天午餐后，随机调查了部分同学就餐饭菜的剩余情况，并将结果统计后绘制成了如图所示的不完整的统计图．
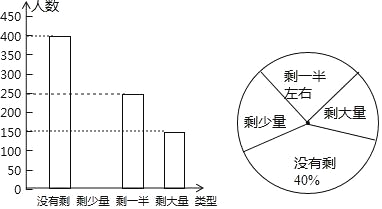
（1）这次被调查的同学共有名；
（2）补全条形统计图；
（3）计算在扇形统计图中剩大量饭菜所对应扇形圆心角的度数；
（4）校学生会通过数据分析，估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐．据此估算，该校20000名学生一餐浪费的食物可供多少人食用一餐？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在菱形ABCD中，AB=BD，点E、F分别是AB、AD上任意的点（不与端点重合），且AE=DF，连接BF与DE相交于点G，连接CG与BD相交于点H．给出如下几个结论：
①∠ADE=∠DBF；②△DAE≌△BDG；③若AF=2DF，则BG=6GF；④CG与BD一定不垂直；⑤∠BGE=60°．其中正确的结论个数为（ ）
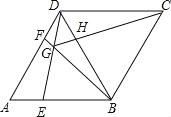
A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某中学决定在“五·四艺术周”为一个节目制作A、B两种道具，共80个． 制作的道具需要甲、乙两种材料组合而成，现有甲种材料700件，乙种材料500件，已知组装A、B两种道具所需的甲、乙两种材料，如下表所示：
甲种材料（件） | 乙种材料（件） | |
A道具 | 6 | 8 |
B道具 | 10 | 4 |
经过计算，制作一个A道具的费用为5元，一个B道具的费用为4.5元． 设组装A种道具x个，所需总费用为y元．
（1）求y与x的函数关系式，并求出x的取值范围；
（2）问组装A种道具多少个时，所需总费用最少，最少费用是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线 
的解析式为
，直线 
的解析式为
，
为上的一点，且点的坐标为
作直线 
轴，交直线于 点
，再作
于点，交直线 于点
，作
轴，交直线于点
，再作
于点
，作
轴，交直线于点
....按此作法继续作下去，则 的坐标为_____，
的坐标为______
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下面材料：
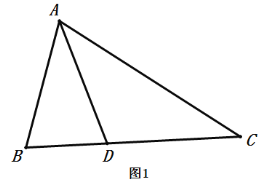
小明遇到这样一个问题：
如图1，在
中，
平分
，
．求证：
小明通过思考发现，可以通过“截长、补短”两种方法解决问题：
方法1：如图2，在
上截取
，使得
，连接
，可以得到全等三角形，进而解决问题
方法二：如图3，延长
到点
，使得
，连接，可以得到等腰三角形，进而解决问题
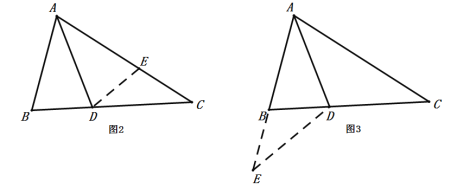
（1）根据阅读材料，任选一种方法证明
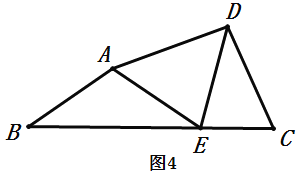
（2）根据自己的解题经验或参考小明的方法，解决下面的问题：如图4，四边形
中，是
上一点，
，
，
，探究
、
、
之间的数量关系，并证明
查看答案和解析>>
科目：初中数学 来源： 题型：
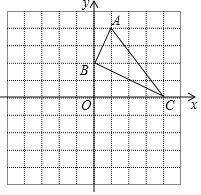
【题目】如图，已知网格上最小的正方形的边长为
（长度单位），点
在格点上.
（1）直接在平面直角坐标系中作出
关于
轴对称的图形
（点
对应点
，点
对应点
）；
（2）的面积为 （面积单位）（直接填空）；
（3）点
到直线
的距离为 （长度单位）（直接填空）；
查看答案和解析>>
科目：初中数学 来源： 题型：
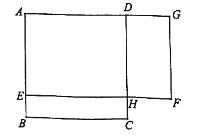
【题目】如图， 
是一块边长为4米的正方形苗圃，园林部门将其改造为矩形
的形状，其中点
在
边上，点
在
的延长线上， 
设
的长为
米，改造后苗圃
的面积为
平方米.
(1) 
与
之间的函数关系式为 （不需写自变量的取值范围）；
(2)根据改造方案，改造后的矩形苗圃
的面积与原正方形苗圃
的面积相等，请问此时
的长为多少米？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
