
【题目】如图,直线 ![]() 的解析式为
的解析式为![]() ,直线
,直线 ![]() 的解析式为
的解析式为![]() ,
,![]() 为
为![]() 上的一点,且
上的一点,且![]() 点的坐标为
点的坐标为![]() 作直线
作直线 ![]() 轴,交直线于
轴,交直线于![]() 点
点![]() ,再作
,再作![]() 于点
于点![]() ,交直线
,交直线 ![]() 于点
于点![]() ,作
,作![]() 轴,交直线于
轴,交直线于![]() 点
点![]() ,再作
,再作![]()
![]() 于点
于点![]() ,作
,作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ....按此作法继续作下去,则
....按此作法继续作下去,则 ![]() 的坐标为_____,
的坐标为_____,![]() 的坐标为______
的坐标为______

科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形ABCD中,E是AB边的中点,DE交AC于点F,AC、DE把它分成的四部分的面积分别为S1S2S3S4,下面结论:
①只有一对相似三角形
②EF:ED=1:2
③S1:S2:S3:S4=1:2:4:5
其中正确的结论是( )
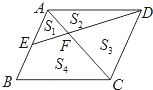
A.①③ B.③ C.① D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,这是一个供滑板爱好者使用的![]() 型池的示意图,该
型池的示意图,该![]() 型池可以看成是长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是直径为
型池可以看成是长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是直径为![]() 的半圆,其边缘
的半圆,其边缘![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,一滑板爱好者从
,一滑板爱好者从![]() 点滑到
点滑到![]() 点,则他滑行的最短距离约为_________
点,则他滑行的最短距离约为_________![]() .(边缘部分的厚度忽略不计)
.(边缘部分的厚度忽略不计)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台的一档娱乐性节目中,在游戏PK环节,为了随机分选游戏双方的组员,主持人设计了以下游戏:用不透明的白布包住三根颜色长短相同的细绳AA1、BB1、CC1,只露出它们的头和尾(如图所示),由甲、乙两位嘉宾分别从白布两端各选一根细绳,并拉出,若两人选中同一根细绳,则两人同队,否则互为反方队员.
(1)若甲嘉宾从中任意选择一根细绳拉出,求他恰好抽出细绳AA1的概率;
(2)请用画树状图法或列表法,求甲、乙两位嘉宾能分为同队的概率.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市出租车计费办法如图所示.根据图象信息,下列说法错误的是( )
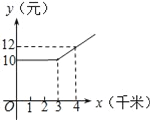
A. 出租车起步价是10元
B. 在3千米内只收起步价
C. 超过3千米部分(x>3)每千米收3元
D. 超过3千米时(x>3)所需费用y与x之间的函数关系式是y=2x+4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们学过的分解因式的方法有提取公因式法、公式法及十字相乘法,但有很多的多项式只用上述方法就无法分解,如![]() ,我们细心观察这个式子就会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式了.过程为:
,我们细心观察这个式子就会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式了.过程为: ![]() ;这种分解因式的方法叫分组分解法.利用这种方法解决下列问题:
;这种分解因式的方法叫分组分解法.利用这种方法解决下列问题:
(1)分解因式:![]()
(2)![]() 三边
三边![]() ,
,![]() ,
,![]() 满足
满足![]() ,判断
,判断![]() 的形状.
的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
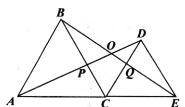
【题目】如图,点![]() 为线段
为线段![]() 上一点,在
上一点,在![]() 同侧分别作正三角形
同侧分别作正三角形![]() 和
和![]() ,
,![]() 分别与
分别与![]() 、
、![]() 交于点
交于点![]() 、
、![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,以下结论:①
,以下结论:①![]() ≌
≌![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .以上结论正确的有_________(把你认为正确的序号都填上).
.以上结论正确的有_________(把你认为正确的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
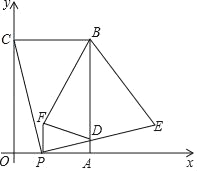
【题目】如图,在平面直角坐标系中,矩形OABC的顶点B坐标为(4,6),点P为线段OA上一动点(与点O、A不重合),连接CP,过点P作PE⊥CP交AB于点D,且PE=PC,过点P作PF⊥OP且PF=PO(点F在第一象限),连结FD、BE、BF,设OP=t.
(1)直接写出点E的坐标(用含t的代数式表示):_____;
(2)四边形BFDE的面积记为S,当t为何值时,S有最小值,并求出最小值;
(3)△BDF能否是等腰直角三角形,若能,求出t;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,隧道的截面由抛物线ADC和矩形AOBC构成,矩形的长OB是12m,宽OA是4m.拱顶D到地面OB的距离是10m.若以O原点,OB所在的直线为x轴,OA所在的直线为y轴,建立直角坐标系.
(1)画出直角坐标系xOy,并求出抛物线ADC的函数表达式;
(2)在抛物线型拱壁E、F处安装两盏灯,它们离地面OB的高度都是8m,则这两盏灯的水平距离EF是多少米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com