
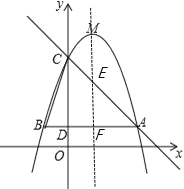
����Ŀ����ͼ����֪���κ���y=��x2+bx+c��b��cΪ��������ͼ����A��3��1������C��0��4��������Ϊ��M������A��AB��x�ᣬ��y���ڵ�D�����ö��κ���ͼ���ڵ�B������BC��

��1����ö��κ����Ľ���ʽ����M�����ꣻ
��2�������ö��κ���ͼ������ƽ��m��m��0������λ��ʹƽ�ƺ�õ��Ķ��κ���ͼ��Ķ���������ABC���ڲ�����������ABC�ı߽�������m��ȡֵ��Χ��
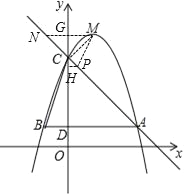
��3����P��ֱ��AC�ϵĶ��㣬����P����C����M�����ɵ�����������BCD���ƣ���ֱ��д�����е�P��������ֱ��д�����������д����������
���𰸡���1��y=��x2+2x+4��M��1,5������2��2��m��4����3��P1��![]() ����P2��
����P2��![]() ����P3��3��1����P4����3��7����
����P3��3��1����P4����3��7����
��������
�����������1������A����C��������뺯������ʽ���������b��c��ֵ��ͨ���䷽���õ���M�����ꣻ��2����M�����ŶԳ���ֱ��x=1����ƽ�Ƶģ��������ֱ��AC�Ľ���ʽ����x=1���������M������ƽ��ʱ��AC��AB�ཻʱy��ֵ�����ɵõ�m��ȡֵ��Χ����3������������ɵ���MCP=90����������PCM����BCD���ƣ���Ҫ���з������ۣ��ֳ���PCM�ס�BDC����PCM�ס�CDB���֣�Ȼ�����ñߵĶ�Ӧ��ֵ��������꣮
�����������1���ѵ�A��3��1������C��0��4��������κ���y=��x2+bx+c�ã�
![]() ���
���![]() �����κ�������ʽΪy=��x2+2x+4�� �䷽��y=����x��1��2+5��
�����κ�������ʽΪy=��x2+2x+4�� �䷽��y=����x��1��2+5��
����M��������1��5����
��2����ֱ��AC����ʽΪy=kx+b���ѵ�A��3��1����C��0��4������ã�![]() ��ã�
��ã�![]()
��ֱ��AC�Ľ���ʽΪy=��x+4����ͼ��ʾ���Գ���ֱ��x=1����ABC���߷ֱ��ڵ�E����F
��x=1����ֱ��AC����ʽy=��x+4���y=3�����E����Ϊ��1��3������F����Ϊ��1��1��
��1��5��m��3�����2��m��4��
��3������MC����MG��y�Ტ�ӳ���AC�ڵ�N�����G����Ϊ��0��5�� ��MG=1��GC=5��4=1
��MC=![]() =
=![]() �� ��y=5����y=��x+4���x=��1�����N��������1��5����
�� ��y=5����y=��x+4���x=��1�����N��������1��5����
��NG=GC��GM=GC�� ���NCG=��GCM=45���� ���NCM=90����
�ɴ˿�֪������P��AC�ϣ�����MCP=90�������D���C��Ϊ���������ζ�Ӧ��
��������PCM�ס�BDC������![]()
��BD=1��CD=3�� ��CP=![]() =
=![]() =
=![]() �� ��CD=DA=3�� ���DCA=45����
�� ��CD=DA=3�� ���DCA=45����
����P��y���Ҳ࣬��PH��y�ᣬ �ߡ�PCH=45����CP=![]() ��PH=
��PH=![]() =
=![]()
��x=![]() ����y=��x+4�����y=
����y=��x+4�����y=![]() �� ��P1��
�� ��P1��![]() ����
����
ͬ���ɵã�����P��y����࣬���x=��![]() ����y=��x+4�����y=
����y=��x+4�����y=![]() ��P2��
��P2��![]() ����
����
��������PCM�ס�CDB������![]() ��CP=
��CP=![]() =3
=3![]() ��PH=3
��PH=3![]() ��
��![]() =3��
=3��
����P��y���Ҳ࣬��x=3����y=��x+4�����y=1��
����P��y����࣬��x=��3����y=��x+4�����y=7
��P3��3��1����P4����3��7����
�����з�������õ�P������4�����ֱ�ΪP1��![]() ����P2��
����P2��![]() ����P3��3��1����P4����3��7����
����P3��3��1����P4����3��7����


 ������ȫ�̼����ĩ���100��ϵ�д�
������ȫ�̼����ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������5�£�ij������ҵ���������ȡ������m����ҵ������������������������갴�������ɼ��ֳ���A��B��C��D�ĸ��ȼ�����������ͼ�в�������ͳ��ͼ����
�����ɼ�n������ | �����ȼ� | Ƶ�� |
90��n��100 | A | 2 |
80��n��90 | B | |
70��n��80 | C | 15 |
n��70 | D | 6 |
����������Ϣ����������⣺
��1����m��ֵ��
��2��������ͳ��ͼ�У���B�ȼ��������ε�Բ�ĽǵĴ�С��������öȡ��֡����ʾ��
��3���������ɼ�������80�ֵ�����������ѡ2�ҽ���Ӫ�����飬������������һ����A�ȼ��ĸ��ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵������ȷ���ǣ�������
A. ���������������ڵ�ֱ�߽���һ��
B. ����ֻ��һ��ֱ������ֱ֪��ƽ��
C. ��ֱ��ͬһ��ֱ�ߵ�����ֱ���ഹֱ
D. ��ֱ����һ�㵽����ֱ�ߵĴ��߶Σ�������㵽����ֱ�ߵľ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺����P��a��b���ں���y=![]() ��ͼ���ϣ�����aΪ������ϵ����bΪһ����ϵ������Ķ��κ���y=ax2+bx��Ϊ����y=
��ͼ���ϣ�����aΪ������ϵ����bΪһ����ϵ������Ķ��κ���y=ax2+bx��Ϊ����y=![]() ��һ�������������������磺�㣨2��
��һ�������������������磺�㣨2�� ![]() ���ں���y=
���ں���y=![]() ��ͼ���ϣ�����y=2x2+
��ͼ���ϣ�����y=2x2+ ![]() ��Ϊ����y=
��Ϊ����y=![]() ��һ�����������������ָ��������������⣺
��һ�����������������ָ��������������⣺
��1�����ں���y=![]() ��һ������������������ͼ��ĶԳ�����y����Ҳ�
��һ������������������ͼ��ĶԳ�����y����Ҳ�
��2������y=![]() ��������������������ͼ����ͬһ�㣬�����ж���ȷ���ǣ�������
��������������������ͼ����ͬһ�㣬�����ж���ȷ���ǣ�������
A. ���⣨1�������⣨2������������
B. ���⣨1�������⣨2�����Ǽ�����
C. ���⣨1���Ǽ����⣬���⣨2����������
D. ���⣨1���������⣬���⣨2���Ǽ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij�����ϻ��������ϻ���ָ��ḣ��Ժ������Ժ�������������ĵȣ������Ȳ��ƽ���ӵ�е����ϴ�λ�������ӣ�
��1�����е����ϴ�λ����![]() ���
���![]() ���������
���������![]() ���
���![]() ���������������꣨��
���������������꣨��![]() ���
���![]() ��ף�ӵ�е����ϴ�λ����ƽ���������ʣ�
��ף�ӵ�е����ϴ�λ����ƽ���������ʣ�
��2��������ij�����������½�һ�������ģ����й滮������������ר�÷��乲![]() �䣬����������ר�÷���ֱ�Ϊ���˼䣨
�䣬����������ר�÷���ֱ�Ϊ���˼䣨![]() �����ϴ�λ����˫�˼䣨
�����ϴ�λ����˫�˼䣨![]() �����ϴ�λ�������˼䣨
�����ϴ�λ�������˼䣨![]() �����ϴ�λ������ʵ����Ҫ�����˼䷿������
�����ϴ�λ������ʵ����Ҫ�����˼䷿������![]() ��
��![]() ֮�䣨����
֮�䣨����![]() ��
��![]() ������˫�˼�ķ������ǵ��˼��
������˫�˼�ķ������ǵ��˼��![]() ������滮���쵥�˼�ķ�����Ϊ
������滮���쵥�˼�ķ�����Ϊ![]() ��
��
�������������Ľ��ɺ���ṩ���ϴ�λ![]() ������
������![]() ��ֵ��
��ֵ��
������������Ľ��ɺ�����ṩ���ϴ�λ���ٸ��������ṩ���ϴ�λ���ٸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=-3(x+2)2�Ķ���������_____________,��������ת180����µ�������,�����ʽΪ________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=ax2+bx+4��x�ύ��A����2��0����B���㣬��y�ύ��C�㣬��Գ���Ϊֱ��x=1��

��1��ֱ��д�������ߵĽ���ʽ�� ��
��2�����߶�AC��x������ƽ�ƣ���ƽ�ƺ�A��C�Ķ�Ӧ��ֱ�ΪA�䡢C�䣬��C��������������ʱ����A�䡢C������ꣻ
��3������2���еĵ�A�䡢C���⣬��x������������Ƿֱ���ڵ�E��F��ʹ����A��C��E��FΪ������ı���Ϊƽ���ı��Σ������ڣ����E��F�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com