
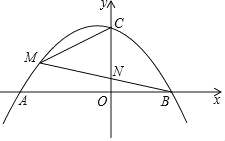
【题目】如图,抛物线y=ax2+ax﹣12a(a<0)与x轴交于A、B两点(A在B的左侧),与y轴交于点C,点M是第二象限内抛物线上一点,BM交y轴于N.
(1)求点A、B的坐标;
(2)若BN=MN,且S△MBC=![]() ,求a的值;
,求a的值;
(3)若∠BMC=2∠ABM,求![]() 的值.
的值.
【答案】(1)A(﹣4,0),B(3,0);(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)设y=0,可求x的值,即求A,B的坐标;
(2)作MD⊥x轴,由CO∥MD可得OD=3,把x=-3代入解析式可得M点坐标,可得ON的长度,根据S△BMC=![]() ,可求a的值;
,可求a的值;
(3)过M点作ME∥AB,设NO=m,![]() =k,可以用m,k表示CO,EO,MD,ME,可求M点坐标,代入可得k,m,a的关系式,由CO=2km+m=-12a,可得方程组,解得k,即可求结果.
=k,可以用m,k表示CO,EO,MD,ME,可求M点坐标,代入可得k,m,a的关系式,由CO=2km+m=-12a,可得方程组,解得k,即可求结果.
(1)设y=0,则0=ax2+ax﹣12a (a<0),
∴x1=﹣4,x2=3,
∴A(﹣4,0),B(3,0)
(2)如图1,作MD⊥x轴,

∵MD⊥x轴,OC⊥x轴,
∴MD∥OC,
∴![]() =
=![]() 且NB=MN,
且NB=MN,
∴OB=OD=3,
∴D(﹣3,0),
∴当x=﹣3时,y=﹣6a,
∴M(﹣3,﹣6a),
∴MD=﹣6a,
∵ON∥MD
∴![]() ,
,
∴ON=﹣3a,
根据题意得:C(0,﹣12a),
∵S△MBC=![]() ,
,
∴![]() (﹣12a+3a)×6=
(﹣12a+3a)×6=![]() ,
,
a=﹣![]() ,
,
(3)如图2:过M点作ME∥AB,
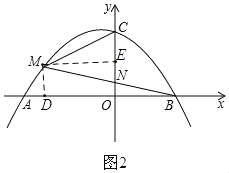
∵ME∥AB,
∴∠EMB=∠ABM且∠CMB=2∠ABM,
∴∠CME=∠NME,且ME=ME,∠CEM=∠NEM=90°,
∴△CME≌△MNE,
∴CE=EN,
设NO=m,![]() =k(k>0),
=k(k>0),
∵ME∥AB,
∴![]() =
=![]() =k,
=k,
∴ME=3k,EN=km=CE,
∴EO=km+m,
CO=CE+EN+ON=2km+m=﹣12a,
即![]() ,
,
∴M(﹣3k,km+m),
∴km+m=a(9k2﹣3k﹣12),
(k+1)×![]() =(k+1)(9k﹣12),
=(k+1)(9k﹣12),
∴![]() =9k-12,
=9k-12,
∴k=![]() ,
,
∴![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】(1)如图①,已知线段![]() ,以
,以![]() 为一边作等边
为一边作等边![]() (尺规作图,保留作图痕迹,不写作法);
(尺规作图,保留作图痕迹,不写作法);
(2)如图②,已知![]() ,
,![]() ,
,![]() ,分别以
,分别以![]() 为边作等边
为边作等边![]() 和等边
和等边![]() ,连接
,连接![]() ,求
,求![]() 的最大值;
的最大值;
(3)如图③,已知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 内部一点,连接
内部一点,连接![]() ,求出
,求出![]() 的最小值.
的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在等边三角形![]() 中,
中,

①如图①,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的点,且
上的点,且![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,则
,则![]() 的度数是___________度;
的度数是___________度;
②如图②,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 延长线上的点,且
延长线上的点,且![]() ,
,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,此时
,此时![]() 的度数是____________度;
的度数是____________度;
(2)如图③,在![]() 中,
中,![]() ,
,![]() 是锐角,点
是锐角,点![]() 是
是![]() 边的垂直平分线与
边的垂直平分线与![]() 的交点,点
的交点,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 的延长线上,且
的延长线上,且![]() ,
,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,若
,若![]() ,求
,求![]() 的大小(用含法
的大小(用含法![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,等边△ABC的边长为3,分别以顶点B、A、C为圆心,BA长为半径作弧AC、弧CB、弧BA,我们把这三条弧所组成的图形称作莱洛三角形,显然莱洛三角形仍然是轴对称图形.设点I为对称轴的交点,如图2,将这个图形的顶点A与等边△DEF的顶点D重合,且AB⊥DE,DE=2π,将它沿等边△DEF的边作无滑动的滚动,当它第一次回到起始位置时,这个图形在运动中扫过区域面积是( )
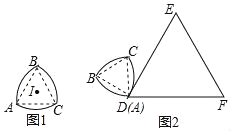
A. 18π B. 27π C. ![]() π D. 45π
π D. 45π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
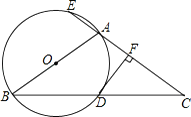
(1)试说明DF是⊙O的切线;
(2)若AC=3AE,求tanC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国移动某套餐推出了如下两种流量计费方式:
月租费/元 | 流量费(元/ | |
方式一 | 8 | 1 |
方式二 | 28 | 0.5 |
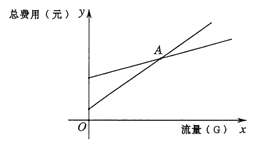
(1)设一个月内用移动电话使用流量为![]() ,方式一总费用
,方式一总费用![]() 元,方式二总费用
元,方式二总费用![]() 元(总费用不计通话费及其它服务费).写出
元(总费用不计通话费及其它服务费).写出![]() 和
和![]() 关于
关于![]() 的函数关系式(不要求写出自变量
的函数关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
(2)如图为在同一平面直角坐标系中画出(1)中的两个函数图象的示意图,记它们的交点为点![]() ,求点
,求点![]() 的坐标,并解释点
的坐标,并解释点![]() 坐标的实际意义;
坐标的实际意义;
(3)根据(2)中函数图象,结合每月使用的流量情况,请直接写出选择哪种计费方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知经过点M(1,4)的直线y = kx+b(k≠0)与直线y = 2x-3平行.
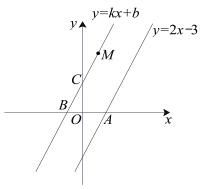
(1)求k,b的值;
(2)若直线y = 2x-3与x轴交于点A,直线y = kx+b交x轴于点B,交y轴于点C,求△MAC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂准备在春节前生产甲、乙两种型号的新年礼盒共 80 万套,两种礼盒的成本和售价如下表所示;
甲 | 乙 | |
成本(元/套) | 25 | 28 |
售价(元/套) | 30 | 38 |
(1)该工厂计划筹资金 2150 万元,且全部用于生产甲乙两种礼盒,则这两种礼盒各生产多少万套?
(2)经过市场调查,该厂决定在原计划的基础上增加生产甲种礼盒![]() 万套,增加生产乙种礼盒
万套,增加生产乙种礼盒![]() 万套(
万套(![]() ,
,![]() 都为正整数),且两种礼盒售完后所获得的总利润恰为 690 万元,请问该工厂有几种生产方案?并写出所有可行的生产方案.
都为正整数),且两种礼盒售完后所获得的总利润恰为 690 万元,请问该工厂有几种生产方案?并写出所有可行的生产方案.
(3)在(2)的情况下,设实际生产的两种礼盒的总成本为![]() 万元,请写出
万元,请写出![]() 与
与![]() 的函数关系式,并求出当
的函数关系式,并求出当 ![]() 为多少时成本
为多少时成本![]() 有最小值,并求出成本
有最小值,并求出成本![]() 的最小值为多少万元?
的最小值为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小刚玩“石头、剪刀、布”的游戏,每一局游戏双方各自随机做出“石头”、“剪刀”、“布”三种手势的一种,规定“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”,相同的手势是和局.
(1)用树形图或列表法计算在一局游戏中两人获胜的概率各是多少?
(2)如果两人约定:只要谁率先胜两局,就成了游戏的赢家.用树形图或列表法求只进行两局游戏便能确定赢家的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com