
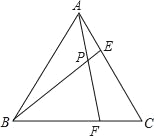
【题目】如图,已知等边△ABC的边长为6,在AC,BC边上各取一点E,F,使AE=CF,连接AF、BE相交于点P,当点E从点A运动到点C时,点P经过点的路径长为__.
科目:初中数学 来源: 题型:
【题目】书店老板去图书批发市场购买某种图书,第一次用 1200 元购买若干本,按 每本 10 元出售,很快售完.第二次购买时,每本书的进价比第一次提高了 20%,他用1500 元所购买的数量比第一次多 10 本.
(1)求第一次购买的图书,每本进价多少元?
(2)第二次购买的图书,按每本 10 元售出 200 本时,出现滞销,剩下的图书降价后全部 售出,要使这两次销售的总利润不低于 2100 元,每本至多降价多少元?(利润=销售收入一进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】意大利文艺复兴时期的著名画家达芬奇利用两张一样的纸片拼出不一样的“空洞”,从而巧妙的证明了勾股定理.小明用两张全等的的纸片①和②拼成如图1所示的图形,中间的六边形![]() 由两个正方形和两个全等的直角三角形组成.已知六边形
由两个正方形和两个全等的直角三角形组成.已知六边形![]() 的面积为28,
的面积为28,![]() .小明将纸片②翻转后拼成如图2所示的图形,其中
.小明将纸片②翻转后拼成如图2所示的图形,其中![]() ,则四边形
,则四边形![]() 的面积为( )
的面积为( )

A.16B.20C.22D.24
查看答案和解析>>
科目:初中数学 来源: 题型:
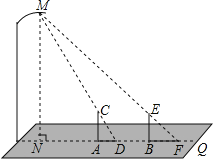
【题目】晚饭后,小林和小京在社区广场散步,两人在灯下沿直线NQ移动,如图,当小林正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小京正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小林的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小京身高BE的长.(结果精确到0.01米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在等边三角形![]() 中,
中,

①如图①,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的点,且
上的点,且![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,则
,则![]() 的度数是___________度;
的度数是___________度;
②如图②,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 延长线上的点,且
延长线上的点,且![]() ,
,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,此时
,此时![]() 的度数是____________度;
的度数是____________度;
(2)如图③,在![]() 中,
中,![]() ,
,![]() 是锐角,点
是锐角,点![]() 是
是![]() 边的垂直平分线与
边的垂直平分线与![]() 的交点,点
的交点,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 的延长线上,且
的延长线上,且![]() ,
,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,若
,若![]() ,求
,求![]() 的大小(用含法
的大小(用含法![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
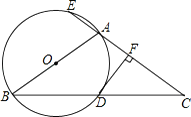
(1)试说明DF是⊙O的切线;
(2)若AC=3AE,求tanC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列满足条件的三角形中,不是直角三角形的是( )
A.三内角之比为1:2:3B.三内角之比为3:4:5
C.三边之比为3:4:5D.三边之比为5:12:13
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com