【题目】意大利文艺复兴时期的著名画家达芬奇利用两张一样的纸片拼出不一样的“空洞”，从而巧妙的证明了勾股定理.小明用两张全等的的纸片①和②拼成如图1所示的图形，中间的六边形
由两个正方形和两个全等的直角三角形组成.已知六边形的面积为28，
.小明将纸片②翻转后拼成如图2所示的图形，其中
，则四边形
的面积为（ ）
A.16B.20C.22D.24
科目：初中数学 来源： 题型：
【题目】（1）如图I，在
中，
.点
在外，连接
，作
，交
于点
，
，
，连接
.则
间的等量关系是______；（不用证明）
（2）如图Ⅱ，
，
，
，延长交
于点，写出间的等量关系，并证明你的结论.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一个拱形桥架可以近似看作是由等腰梯形ABD8D1和其上方的抛物线D1OD8组成.若建立如图所示的直角坐标系，跨度AB=44米，∠A=45°，AC1=4米，点D2的坐标为(-13，-1.69)，则桥架的拱高OH=________米.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）探究新知：如图1，已知△ABC与△ABD的面积相等，试判断AB与CD的位置关系，并说明理由．
（2）结论应用：① 如图2，点M，N在反比例函数
（k＞0）的图象上，过点M作ME⊥y轴，过点N作NF⊥x轴，垂足分别为E，F．试证明：MN∥EF．
② 若①中的其他条件不变，只改变点M，N的位置如图3所示，请判断 MN与EF是否平行？请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某甜品店用
，
两种原料制作成甲、乙两款甜品进行销售，制作每份甜品的原料所需用量如下表所示.该店制作甲款甜品
份，乙款甜品
份，共用去原料2000克．
原料 款式 |
（克） |
（克） |
甲款甜品 | 30 | 15 |
乙款甜品 | 10 | 20 |
（1）求关于的函数表达式；
（2）已知每份甲甜品的利润为5元，每份乙甜品的利润为2元.假设两款甜品均能全部卖出.若获得总利润不少于360元，则至少要用去原料多少克？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知等边△ABC的边长为6，在AC，BC边上各取一点E，F，使AE=CF，连接AF、BE相交于点P，当点E从点A运动到点C时，点P经过点的路径长为__．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①，在正方形ABCD中，点E与点F分别在线段AC、BC上，且四边形DEFG是正方形．
（1）试探究线段AE与CG的关系，并说明理由．
（2）如图②若将条件中的四边形ABCD与四边形DEFG由正方形改为矩形，AB=3，BC=4．
①线段AE、CG在（1）中的关系仍然成立吗？若成立，请证明，若不成立，请写出你认为正确的关系，并说明理由．
②当△CDE为等腰三角形时，求CG的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明随机抽取了某校八年级部分学生，针对他们晚上在家学习时间的情况进行调查，并将调查结果绘制成如下两幅尚不完整的统计图．根据以上信息，解答下列问题：
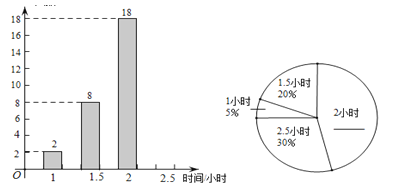
（1）补全条形统计图和扇形统计图；
（2）本次抽取的八年级学生晚上学习时间的众数是 小时，中位数是 小时；
（3）若该校共有 600 名八年级学生，则晚上学习时间超过 1.5 小时的约有多少名学生？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
