
【题目】小明随机抽取了某校八年级部分学生,针对他们晚上在家学习时间的情况进行调查,并将调查结果绘制成如下两幅尚不完整的统计图.根据以上信息,解答下列问题:
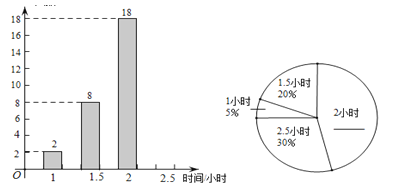
(1)补全条形统计图和扇形统计图;
(2)本次抽取的八年级学生晚上学习时间的众数是 小时,中位数是 小时;
(3)若该校共有 600 名八年级学生,则晚上学习时间超过 1.5 小时的约有多少名学生?
【答案】(1)补全条形统计图和扇形统计图见解析;(2)2,2;(3)晚上学习时间超过 1.5 小时的约有450名学生.
【解析】
(1)先由1小时的人数及其所占百分比求得总人数,总人数乘以2.5小时对应百分比求得其人数,用2小时人数除以总人数可得其百分比;
(2)根据人数、中位数的定义求解可得;
(3)总人数乘以样本中2小时和2.5小时人数所占百分比之和可得.
(1)分别由条形统计图和扇形统计图知:1小时的人数为2人、所占百分比为5%,
∴被调查的学生总人数为2÷5%=40人,
∴2.5小时的人数为40×30%=12人,
2小时人数所占百分比为![]()
补全条形统计图和扇形统计图如下:
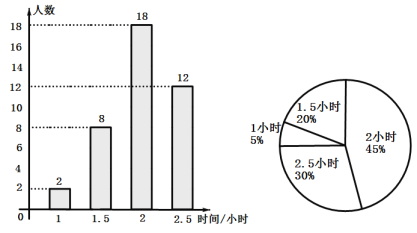
(2)2小时出现的次数最多,是18次,因此众数是2小时,
把这40个数据从小到大排列后处在第20、21位的数都是2,因此中位数是2小时,
故答案为:2,2;
(3)晚上学习时间超过1.5小时的学生约有![]() (人)
(人)
答:晚上学习时间超过 1.5 小时的约有450名学生.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案科目:初中数学 来源: 题型:
【题目】意大利文艺复兴时期的著名画家达芬奇利用两张一样的纸片拼出不一样的“空洞”,从而巧妙的证明了勾股定理.小明用两张全等的的纸片①和②拼成如图1所示的图形,中间的六边形![]() 由两个正方形和两个全等的直角三角形组成.已知六边形
由两个正方形和两个全等的直角三角形组成.已知六边形![]() 的面积为28,
的面积为28,![]() .小明将纸片②翻转后拼成如图2所示的图形,其中
.小明将纸片②翻转后拼成如图2所示的图形,其中![]() ,则四边形
,则四边形![]() 的面积为( )
的面积为( )

A.16B.20C.22D.24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
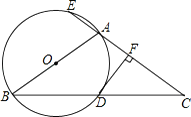
(1)试说明DF是⊙O的切线;
(2)若AC=3AE,求tanC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知经过点M(1,4)的直线y = kx+b(k≠0)与直线y = 2x-3平行.
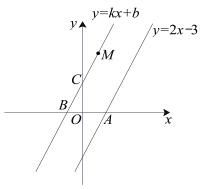
(1)求k,b的值;
(2)若直线y = 2x-3与x轴交于点A,直线y = kx+b交x轴于点B,交y轴于点C,求△MAC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂准备在春节前生产甲、乙两种型号的新年礼盒共 80 万套,两种礼盒的成本和售价如下表所示;
甲 | 乙 | |
成本(元/套) | 25 | 28 |
售价(元/套) | 30 | 38 |
(1)该工厂计划筹资金 2150 万元,且全部用于生产甲乙两种礼盒,则这两种礼盒各生产多少万套?
(2)经过市场调查,该厂决定在原计划的基础上增加生产甲种礼盒![]() 万套,增加生产乙种礼盒
万套,增加生产乙种礼盒![]() 万套(
万套(![]() ,
,![]() 都为正整数),且两种礼盒售完后所获得的总利润恰为 690 万元,请问该工厂有几种生产方案?并写出所有可行的生产方案.
都为正整数),且两种礼盒售完后所获得的总利润恰为 690 万元,请问该工厂有几种生产方案?并写出所有可行的生产方案.
(3)在(2)的情况下,设实际生产的两种礼盒的总成本为![]() 万元,请写出
万元,请写出![]() 与
与![]() 的函数关系式,并求出当
的函数关系式,并求出当 ![]() 为多少时成本
为多少时成本![]() 有最小值,并求出成本
有最小值,并求出成本![]() 的最小值为多少万元?
的最小值为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列满足条件的三角形中,不是直角三角形的是( )
A.三内角之比为1:2:3B.三内角之比为3:4:5
C.三边之比为3:4:5D.三边之比为5:12:13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AD=4,AB=2![]() ,将矩形ABCD绕点A逆时针旋转α(0<α<90°)得到矩形AEFG.延长CB与EF交于点H.
,将矩形ABCD绕点A逆时针旋转α(0<α<90°)得到矩形AEFG.延长CB与EF交于点H.
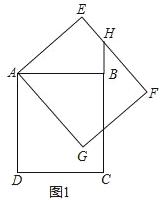
(1)求证:BH=EH;
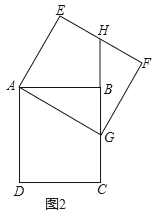
(2)如图2,当点G落在线段BC上时,求点B经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
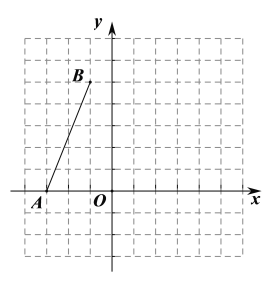
【题目】如图,在平面直角坐标系中,点![]() ,点
,点![]() .
.
(1)①画出线段![]() 关于
关于![]() 轴对称的线段
轴对称的线段![]() ;
;
②在![]() 轴上找一点
轴上找一点![]() 使
使![]() 的值最小(保留作图痕迹);
的值最小(保留作图痕迹);
(2)按下列步骤,用不带刻度的直尺在线段![]() 找一点
找一点![]() 使
使![]() .
.
①在图中取点![]() ,使得
,使得![]() ,且
,且![]() ,则点
,则点![]() 的坐标为___________;
的坐标为___________;
②连接![]() 交
交![]() 于点
于点![]() ,则点
,则点![]() 即为所求.
即为所求.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com