
【题目】如图,等腰三角形![]() 的底边
的底边![]() 长为
长为![]() ,面积是
,面积是![]() ,腰
,腰![]() 的垂直平分线
的垂直平分线![]() 分别交
分别交![]() ,
,![]() 边于
边于![]() ,
,![]() 点.若点
点.若点![]() 为
为![]() 边的中点,点
边的中点,点![]() 为线段
为线段![]() 上一动点,则
上一动点,则![]() 周长的最小值为_________.
周长的最小值为_________.

 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图所示,已知抛物线y=ax2+bx+c(a≠0)经过点A(﹣2,0)、B(4,0)、C(0,﹣8),与直线y=x﹣4交于B,D两点
(1)求抛物线的解析式并直接写出D点的坐标;
(2)点P为直线BD下方抛物线上的一个动点,试求出△BDP面积的最大值及此时点P的坐标;
(3)点Q是线段BD上异于B、D的动点,过点Q作QF⊥x轴于点F,交抛物线于点G,当△QDG为直角三角形时,直接写出点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC的边长为6,在AC,BC边上各取一点E,F,使AE=CF,连接AF、BE相交于点P,当点E从点A运动到点C时,点P经过点的路径长为__.
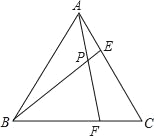
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,BE=AF.
(1)求证:四边形ADEF是平行四边形;
(2)若∠ABC=60°,BD=6,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在正方形ABCD中,点E与点F分别在线段AC、BC上,且四边形DEFG是正方形.


(1)试探究线段AE与CG的关系,并说明理由.
(2)如图②若将条件中的四边形ABCD与四边形DEFG由正方形改为矩形,AB=3,BC=4.
①线段AE、CG在(1)中的关系仍然成立吗?若成立,请证明,若不成立,请写出你认为正确的关系,并说明理由.
②当△CDE为等腰三角形时,求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
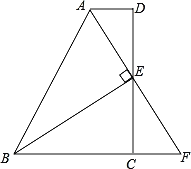
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;(2)AB=BC+AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,平面内互相垂直且有公共原点的两条数轴构成平面直角坐标系,如果两条数轴不垂直,而是相交成任意的角ω(0°<ω<180°且ω≠90°),那么这两条数轴构成的是平面斜坐标系,两条数轴称为斜坐标系的坐标轴,公共原点称为斜坐标系的原点,如图1,经过平面内一点P作坐标轴的平行线PM和PN,分别交x轴和y轴于点M,N.点M、N在x轴和y轴上所对应的数分别叫做P点的x坐标和y坐标,有序实数对(x,y)称为点P的斜坐标,记为P(x,y).
(1)如图2,ω=45°,矩形OABC中的一边OA在x轴上,BC与y轴交于点D,OA=2,OC=l.
①点A、B、C在此斜坐标系内的坐标分别为A ,B ,C .
②设点P(x,y)在经过O、B两点的直线上,则y与x之间满足的关系为 .
③设点Q(x,y)在经过A、D两点的直线上,则y与x之间满足的关系为 .
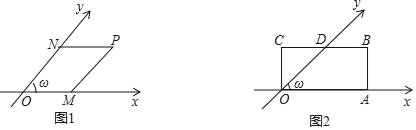
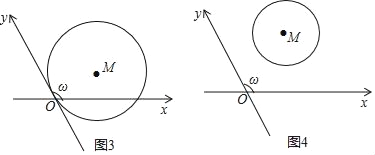
(2)若ω=120°,O为坐标原点.
①如图3,圆M与y轴相切原点O,被x轴截得的弦长OA=4![]() ,求圆M的半径及圆心M的斜坐标.
,求圆M的半径及圆心M的斜坐标.
②如图4,圆M的圆心斜坐标为M(2,2),若圆上恰有两个点到y轴的距离为1,则圆M的半径r的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
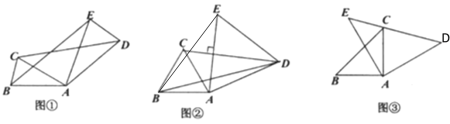
【题目】如图,![]() 和
和![]() 都是等腰三角形,其中
都是等腰三角形,其中![]() ,
,![]() ,且
,且![]() .
.
(1)如图①,连接![]() 、
、![]() ,求证:
,求证:![]() ;
;
(2)如图②,连接![]() 、
、![]() ,若
,若![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长;
的长;
(3)如图③,若![]() ,且
,且![]() 点恰好落在
点恰好落在![]() 上,试探究
上,试探究![]() 、
、![]() 和
和![]() 之间的数量关系,并加以说明.
之间的数量关系,并加以说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com