
【题目】如图,![]() 和
和![]() 都是等腰三角形,其中
都是等腰三角形,其中![]() ,
,![]() ,且
,且![]() .
.
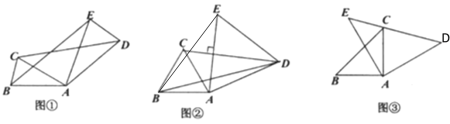
(1)如图①,连接![]() 、
、![]() ,求证:
,求证:![]() ;
;
(2)如图②,连接![]() 、
、![]() ,若
,若![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长;
的长;
(3)如图③,若![]() ,且
,且![]() 点恰好落在
点恰好落在![]() 上,试探究
上,试探究![]() 、
、![]() 和
和![]() 之间的数量关系,并加以说明.
之间的数量关系,并加以说明.
【答案】(1)见解析;(2)5;(3)![]() +
+![]() =
=![]() ,理由见解析
,理由见解析
【解析】
(1)根据等式的基本性质可得∠BAE=∠CAD,然后利用SAS即可证出△BAE≌△CAD,从而证出结论;
(2)根据等式的基本性质可得∠BAE=∠CAD,然后利用SAS即可证出△BAE≌△CAD,然后根据全等三角形的性质可得![]() ,∠BEA=∠CDA,证出△ADE为等边三角形,根据三线合一即可证出∠BED=90°,根据勾股定理即可求出BD;
,∠BEA=∠CDA,证出△ADE为等边三角形,根据三线合一即可证出∠BED=90°,根据勾股定理即可求出BD;
(3)根据等式的基本性质可得∠BAE=∠CAD,然后利用SAS即可证出△BAE≌△CAD,然后根据全等三角形的性质可得![]() ,∠BEA=∠D,证出△ADE为等腰直角三角形即可求出∠BEC=90°,根据勾股定理即可得出结论.
,∠BEA=∠D,证出△ADE为等腰直角三角形即可求出∠BEC=90°,根据勾股定理即可得出结论.
解:(1)∵![]()
∴∠BAC+∠CAE=∠DAE+∠CAE
∴∠BAE=∠CAD
在△BAE和△CAD中

∴△BAE≌△CAD
∴![]()
(2)∵![]()
∴∠BAC+∠CAE=∠DAE+∠CAE
∴∠BAE=∠CAD
在△BAE和△CAD中

∴△BAE≌△CAD
∴![]() ,∠BEA=∠CDA
,∠BEA=∠CDA
∵∠DAE=60°,AE=AD
∴△ADE为等边三角形
∴∠ADE=∠AED=60°,DE=AD=3
∵![]()
∴∠CDA=∠CDE=![]()
∴∠BEA=30°
∴∠BED=∠BEA+∠AED=90°,
在Rt△BED中,BD=![]()

(3)![]() +
+![]() =
=![]() ,理由如下
,理由如下
连接![]() ,
,

∵![]() =90°
=90°
∴∠BAC-∠CAE=∠DAE-∠CAE
∴∠BAE=∠CAD
在△BAE和△CAD中

∴△BAE≌△CAD
∴![]() ,∠BEA=∠D
,∠BEA=∠D
∵∠DAE=90°,AE=AD
∴△ADE为等腰直角三角形
∴∠D=∠AED=45°,
∴∠BEA=45°
∴∠BEC=∠BEA+∠AED=90°
∴在Rt△BEC中,![]() +
+![]() =
=![]()
∴![]() +
+![]() =
=![]()


科目:初中数学 来源: 题型:
【题目】下列满足条件的三角形中,不是直角三角形的是( )
A.三内角之比为1:2:3B.三内角之比为3:4:5
C.三边之比为3:4:5D.三边之比为5:12:13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼AB的高为16m,远处有一塔CD,小李在楼底A处测得塔顶D处的仰角为 60°,在楼顶B处测得塔顶D处的仰角为45°,其中A、C两点分别位于B、D两点正下方,且A、C两点在同一水平线上,求塔CD的高.(![]() =1.73,结果保留一位小数.)
=1.73,结果保留一位小数.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AD=4,AB=2![]() ,将矩形ABCD绕点A逆时针旋转α(0<α<90°)得到矩形AEFG.延长CB与EF交于点H.
,将矩形ABCD绕点A逆时针旋转α(0<α<90°)得到矩形AEFG.延长CB与EF交于点H.
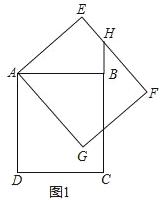
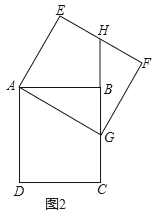
(1)求证:BH=EH;
(2)如图2,当点G落在线段BC上时,求点B经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数 y=x+1 的图象与 y 轴交于点 A,一次函数 y=kx+b 的图象经过点 B(0,﹣1),与x 轴 以及 y=x+1 的图象分别交于点 C、D,且点 D 的坐标为(1,n),

(1)则n= ,k= ,b= ;
(2)函数 y=kx+b 的函数值大于函数 y=x+1 的函数值,则X的取值范围是 ;
(3)求四边形 AOCD 的面积;
(4)在 x轴上是否存在点 P,使得以点 P,C,D 为顶点的三角形是直角三角形?若存在求出点 P 的坐标; 若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
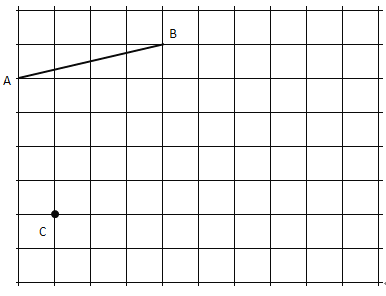
【题目】如图是10×8的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长都是1个单位,线段![]() 的端点均在格点上,且
的端点均在格点上,且![]() 点的坐标为
点的坐标为![]() ,按下列要求用没有刻度的直尺画出图形.
,按下列要求用没有刻度的直尺画出图形.
(1)请在图中找到原点![]() 的位置,并建立平面直角坐标系;
的位置,并建立平面直角坐标系;
(2)将线段![]() 平移到
平移到![]() 的位置,使
的位置,使![]() 与
与![]() 重合,画出线段
重合,画出线段![]() ,然后作线段
,然后作线段![]() 关于直线
关于直线![]() 对称线段
对称线段![]() ,使
,使![]() 的对应点为
的对应点为![]() ,画出线段
,画出线段![]() ;
;
(3)在图中找到一个各点![]() 使
使![]() ,画出
,画出![]() 并写出
并写出![]() 点的坐标.
点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com