
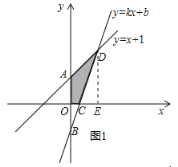
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖŗÆŹż y=x+1 µÄĶ¼ĻóÓė y Öį½»ÓŚµć A£¬Ņ»“ĪŗÆŹż y=kx+b µÄĶ¼Ļó¾¹żµć B£Ø0£¬©1£©£¬Óėx Öį ŅŌ¼° y=x+1 µÄĶ¼Ļó·Ö±š½»ÓŚµć C”¢D£¬ĒŅµć D µÄ×ų±źĪŖ£Ø1£¬n£©£¬

£Ø1£©Ōņn= £¬k= £¬b= £»
£Ø2£©ŗÆŹż y=kx+b µÄŗÆŹżÖµ“óÓŚŗÆŹż y=x+1 µÄŗÆŹżÖµ£¬ŌņXµÄȔֵ·¶Ī§ŹĒ £»
£Ø3£©ĒóĖıߊĪ AOCD µÄĆ껿£»
£Ø4£©ŌŚ xÖįÉĻŹĒ·ń“ęŌŚµć P£¬Ź¹µĆŅŌµć P£¬C£¬D ĪŖ¶„µćµÄČż½ĒŠĪŹĒÖ±½ĒČż½ĒŠĪ£æČō“ęŌŚĒó³öµć P µÄ×ų±ź£» Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ£Ø1£©2£¬3£¬-1£»£Ø2£©![]() £»£Ø3£©
£»£Ø3£©![]() £Ø4£©
£Ø4£©![]() »ņ
»ņ![]()
”¾½āĪö”æ
ŹŌĢā·ÖĪö£ŗ£Ø1£©¶ŌÓŚÖ±Ļß![]() £¬Įī
£¬Įī![]() Ēó³ö
Ēó³ö![]() µÄÖµ£¬Č·¶Ø³öAµÄ×ų±ź£¬°ŃB×ų±ź“śČė
µÄÖµ£¬Č·¶Ø³öAµÄ×ų±ź£¬°ŃB×ų±ź“śČė![]() ÖŠĒó³öbµÄÖµ£¬ŌŁ½«D×ų±ź“śČė
ÖŠĒó³öbµÄÖµ£¬ŌŁ½«D×ų±ź“śČė![]() Ēó³önµÄÖµ£¬½ų¶ų½«D×ų±ź“śČėĒó³ö
Ēó³önµÄÖµ£¬½ų¶ų½«D×ų±ź“śČėĒó³ö![]() µÄÖµ¼“æÉ£»
µÄÖµ¼“æÉ£»
ÓÉĮ½øöŅ»“ĪŗÆŹż½āĪöŹ½£¬½įŗĻĶ¼ĻóČ·¶Ø³ö![]() µÄ·¶Ī§£»
µÄ·¶Ī§£»
¹żD×÷![]() “¹Ö±ÓŚ
“¹Ö±ÓŚ![]() Öį£¬ĖıߊĪ
Öį£¬ĖıߊĪ![]() µÄĆ껿µČÓŚĢŻŠĪ
µÄĆ껿µČÓŚĢŻŠĪ![]() Ć껿¼õČ„Čż½ĒŠĪ
Ć껿¼õČ„Čż½ĒŠĪ![]() Ć껿£¬Ēó³ö¼“æÉ£»
Ć껿£¬Ēó³ö¼“æÉ£»
ŌŚ![]() ÖįÉĻ“ęŌŚµćP£¬Ź¹µĆŅŌµćP”¢C”¢DĪŖ¶„µćµÄČż½ĒŠĪŹĒÖ±½ĒČż½ĒŠĪ£¬ĄķÓÉ£ŗ·ÖĮ½ÖÖĒéæöæ¼ĀĒ£ŗ
ÖįÉĻ“ęŌŚµćP£¬Ź¹µĆŅŌµćP”¢C”¢DĪŖ¶„µćµÄČż½ĒŠĪŹĒÖ±½ĒČż½ĒŠĪ£¬ĄķÓÉ£ŗ·ÖĮ½ÖÖĒéæöæ¼ĀĒ£ŗ![]() £»
£»![]() £¬·Ö±šĒó³öPµć×ų±ź¼“æÉ£®
£¬·Ö±šĒó³öPµć×ų±ź¼“æÉ£®
ŹŌĢā½āĪö£ŗ£Ø1£©¶ŌÓŚÖ±Ļß![]() £¬Įī
£¬Įī![]() µĆµ½
µĆµ½![]() £¬¼“A£Ø0£¬1£©£¬°ŃB£Ø0£¬-1£©“śČė
£¬¼“A£Ø0£¬1£©£¬°ŃB£Ø0£¬-1£©“śČė![]() ÖŠ£¬µĆ£ŗ
ÖŠ£¬µĆ£ŗ![]() £¬°ŃD£Ø1£¬n£©“śČė
£¬°ŃD£Ø1£¬n£©“śČė![]() µĆ£ŗ
µĆ£ŗ![]() £¬¼“D£Ø1£¬2£©£¬°ŃD×ų±ź“śČė
£¬¼“D£Ø1£¬2£©£¬°ŃD×ų±ź“śČė![]() ÖŠµĆ£ŗ
ÖŠµĆ£ŗ![]() £¬¼“
£¬¼“![]() £¬¹Ź“š°øĪŖ£ŗ2£¬3£¬-1£»
£¬¹Ź“š°øĪŖ£ŗ2£¬3£¬-1£»
Ņ»“ĪŗÆŹż![]() Óė
Óė![]() ½»ÓŚµćD£Ø1£¬2£©£¬ÓÉĶ¼ĻóµĆ£ŗŗÆŹż
½»ÓŚµćD£Ø1£¬2£©£¬ÓÉĶ¼ĻóµĆ£ŗŗÆŹż![]() µÄŗÆŹżÖµ“óÓŚŗÆŹż
µÄŗÆŹżÖµ“óÓŚŗÆŹż![]() µÄŗÆŹżÖµ
µÄŗÆŹżÖµ![]() Ź±µÄȔֵ·¶Ī§ŹĒ
Ź±µÄȔֵ·¶Ī§ŹĒ![]() £»¹Ź“š°øĪŖ£ŗ
£»¹Ź“š°øĪŖ£ŗ![]() £»
£»
¹żD×÷![]() “¹Ö±ÓŚ
“¹Ö±ÓŚ![]() Öį£¬ČēĶ¼1ĖłŹ¾£¬Ōņ
Öį£¬ČēĶ¼1ĖłŹ¾£¬Ōņ![]()
![]()
![]()
£Ø4£©ČēĶ¼2£¬ŌŚ![]() ÖįÉĻ“ęŌŚµćP£¬Ź¹µĆŅŌµćP”¢C”¢DĪŖ¶„µćµÄČż½ĒŠĪŹĒÖ±½ĒČż½ĒŠĪ£¬ĄķÓÉ£ŗ·ÖĮ½ÖÖĒéæöæ¼ĀĒ£ŗµ±
ÖįÉĻ“ęŌŚµćP£¬Ź¹µĆŅŌµćP”¢C”¢DĪŖ¶„µćµÄČż½ĒŠĪŹĒÖ±½ĒČż½ĒŠĪ£¬ĄķÓÉ£ŗ·ÖĮ½ÖÖĒéæöæ¼ĀĒ£ŗµ±![]() Ź±£¬æɵĆ
Ź±£¬æɵĆ![]()
![]() Š±ĀŹĪŖ3£¬
Š±ĀŹĪŖ3£¬![]() Š±ĀŹĪŖ
Š±ĀŹĪŖ![]() £¬
£¬![]()
![]() ½āĪöŹ½ĪŖ
½āĪöŹ½ĪŖ![]() Įī
Įī![]() ¼“
¼“![]() µ±
µ±![]() Ź±£¬ÓÉDŗį×ų±źĪŖ1£¬µĆµ½Pµćŗį×ų±źĪŖ1£¬
Ź±£¬ÓÉDŗį×ų±źĪŖ1£¬µĆµ½Pµćŗį×ų±źĪŖ1£¬![]() ŌŚ
ŌŚ![]() ÖįÉĻ£¬
ÖįÉĻ£¬![]()




| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
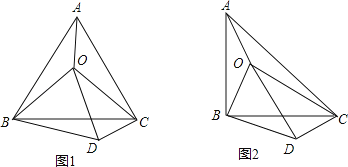
”¾ĢāÄæ”æ£Ø1£©ČēĶ¼1£¬OŹĒµČ±ß”÷ABCÄŚŅ»µć£¬Į¬½ÓOA”¢OB”¢OC£¬ĒŅOA=3£¬OB=3£¬OC=5£¬½«”÷BAOČʵćBĖ³Ź±ÕėŠż×ŖŗóµĆµ½”÷BCD£¬Į¬½ÓOD£®Ēó£ŗ
¢ŁŠż×Ŗ½ĒµÄ¶ČŹż£»
¢ŚĻ߶ĪODµÄ³¤£»
¢Ū”ĻBDCµÄ¶ČŹż£®
£Ø2£©ČēĶ¼2ĖłŹ¾£¬OŹĒµČŃüÖ±½Ē”÷ABC£Ø”ĻABC=90”ć£©ÄŚŅ»µć£¬Į¬½ÓOA”¢OB”¢OC£¬½«”÷BAOČʵćBĖ³Ź±ÕėŠż×ŖŗóµĆµ½”÷BCD£¬Į¬½ÓOD£®µ±OA”¢OB”¢OCĀś×ćŹ²Ć“Ģõ¼žŹ±£¬”ĻODC=90”ć£æĒėøų³öÖ¤Ć÷£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖµć£Øa£¬1£©ŌŚŗÆŹży=3x+4µÄĶ¼ĻóÉĻ£¬Ōņa=____________£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
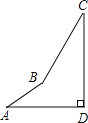
”¾ĢāÄæ”æČēĶ¼£¬AD”ĶCD£¬AB=10£¬BC=20£¬”ĻA=”ĻC=30”ć£¬ĒóAD”¢CDµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”抔ĮĮµÄĢåÖŲĪŖ43.95kg£¬¾«Č·µ½0.1kgĖłµĆ½üĖĘÖµĪŖ__________
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ(2016ĖÄ“ØŹ”ĄÖɽŹŠµŚ3Ģā)ij°ąæŖÕ¹1·ÖÖÓŃöĪŌĘš×ų±ČČü»ī¶Æ£¬5ĆūĶ¬Ń§µÄ³É¼ØČēĻĀ£Øµ„Ī»£ŗøö£©£ŗ37”¢38”¢40”¢40”¢42£®Õā×鏿¾ŻµÄÖŚŹżŹĒ£Ø £©
A£®37 B£®38 C£®40 D£®42
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĮŠÓļ¾äŹĒÕęĆüĢāµÄŹĒ£Ø £©
A. ¶Ō¶„½ĒĻąµČ B. µ×±ßĻąµČµÄĮ½øöµČŃüČż½ĒŠĪČ«µČ
C. ŅŃÖŖa2=4£¬ĒóaµÄÖµ D. Čōa>b£¬Ōņa2£¾b2
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ
£Ø1£©ĒóĮ½øö¶ÆµćŌĖ¶ÆµÄĖŁ¶Č£»
£Ø2£©ŌŚŹżÖįÉĻ±ź³öA”¢BĮ½µć“ÓŌµć³ö·¢ŌĖ¶Æ2ĆėŹ±µÄĪ»ÖĆ£»
£Ø3£©Čō±ķŹ¾Źż0µÄµć¼ĒĪŖO£¬A”¢BĮ½µć·Ö±š“Ó£Ø2£©ÖŠ±ź³öµÄĪ»ÖĆĶ¬Ź±ĻņŹżÖįøŗ·½ĻņŌĖ¶Æ£¬ŌŁ¾¹ż¶ą³¤Ź±¼ä£¬OB=2OA£®
![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬A£Ø1£¬3£©£¬B£Ø2£¬4£©£¬C£Ø3£¬5£©£¬D£Ø4£¬6£©ĘäÖŠ²»ÓėE£Ø2£¬-3£©ŌŚĶ¬Ņ»øöŗÆŹżĶ¼ĻńÉĻµÄŅ»øöµćŹĒ£Ø £©
A. µćA B. µćB C. µćC D. µćD
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com