
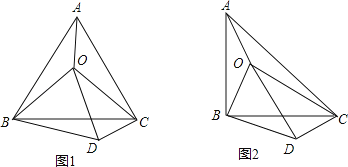
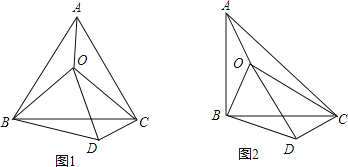
【题目】(1)如图1,O是等边△ABC内一点,连接OA、OB、OC,且OA=3,OB=3,OC=5,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.求:
①旋转角的度数;
②线段OD的长;
③∠BDC的度数.
(2)如图2所示,O是等腰直角△ABC(∠ABC=90°)内一点,连接OA、OB、OC,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.当OA、OB、OC满足什么条件时,∠ODC=90°?请给出证明.
【答案】(1)①60°;②OD=OB=4;③150°;(2)当OA、OB、OC满足OA2+2OB2=OC2时,∠ODC=90°.
【解析】
试题分析:(1)①根据等边三角形的性质得BA=BC,∠ABC=60°,再根据旋转的性质得∠OBD=∠ABC=60°,于是可确定旋转角的度数为60°;
②由旋转的性质得BO=BD,加上∠OBD=60°,则可判断△OBD为等边三角形,所以OD=OB=4;
③由△BOD为等边三角形得到∠BDO=60°,再利用旋转的性质得CD=AO=3,然后根据勾股定理的逆定理可证明△OCD为直角三角形,∠ODC=90°,所以∠BDC=∠BDO+∠ODC=150°;
(2)根据旋转的性质得∠OBD=∠ABC=90°,BO=BD,CD=AO,则可判断△OBD为等腰直角三角形,则OD=![]() OB,然后根据勾股定理的逆定理,当CD2+OD2=OC2时,△OCD为直角三角形,∠ODC=90°.
OB,然后根据勾股定理的逆定理,当CD2+OD2=OC2时,△OCD为直角三角形,∠ODC=90°.
解:(1)①∵△ABC为等边三角形,
∴BA=BC,∠ABC=60°,
∵△BAO绕点B顺时针旋转后得到△BCD,
∴∠OBD=∠ABC=60°,
∴旋转角的度数为60°;
②∵△BAO绕点B顺时针旋转后得到△BCD,
∴BO=BD,
而∠OBD=60°,
∴△OBD为等边三角形;
∴OD=OB=4;
③∵△BOD为等边三角形,
∴∠BDO=60°,
∵△BAO绕点B顺时针旋转后得到△BCD,
∴CD=AO=3,
在△OCD中,CD=3,OD=4,OC=5,
∵32+42=52,
∴CD2+OD2=OC2,
∴△OCD为直角三角形,∠ODC=90°,
∴∠BDC=∠BDO+∠ODC=60°+90°=150°;
(2)OA2+2OB2=OC2时,∠ODC=90°.理由如下:
∵△BAO绕点B顺时针旋转后得到△BCD,
∴∠OBD=∠ABC=90°,BO=BD,CD=AO,
∴△OBD为等腰直角三角形,
∴OD=![]() OB,
OB,
∵当CD2+OD2=OC2时,△OCD为直角三角形,∠ODC=90°,
∴OA2+2OB2=OC2,
∴当OA、OB、OC满足OA2+2OB2=OC2时,∠ODC=90°.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案科目:初中数学 来源: 题型:
【题目】某校为了解学生对三种国庆活动方案的意见,对该校学生进行了一次抽样调查(被调查学生至多赞成其中的一种方案),现将调查结果绘制成如图两幅不完整的统计图.请根据图中提供的信息解答下列问题

(1)这次共调查了多少名学生?扇形统计图中方案1所对应的圆心角的度数为多少度?
(2)请把条形统计图补充完整;
(3)已知该校有1000名学生,试估计该校赞成方案1的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC为等边三角形,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则四个结论正确的是( )
①点P在∠A的平分线上;
②AS=AR;
③QP∥AR;
④△BRP≌△QSP.
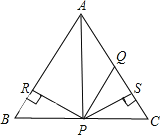
A.全部正确 B.仅①和②正确 C.仅②③正确 D.仅①和③正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. 数轴上的点与有理数一一对应 B. 数轴上的点与无理数一一对应
C. 数轴上的点与整数一一对应 D. 数轴上的点与实数一一对应
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016湖南省邵阳市第7题)一元二次方程2x2﹣3x+1=0的根的情况是( )
A.有两个相等的实数根 B.有两个不相等的实数根
C.只有一个实数根 D.没有实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数 y=x+1 的图象与 y 轴交于点 A,一次函数 y=kx+b 的图象经过点 B(0,﹣1),与x 轴 以及 y=x+1 的图象分别交于点 C、D,且点 D 的坐标为(1,n),

(1)则n= ,k= ,b= ;
(2)函数 y=kx+b 的函数值大于函数 y=x+1 的函数值,则X的取值范围是 ;
(3)求四边形 AOCD 的面积;
(4)在 x轴上是否存在点 P,使得以点 P,C,D 为顶点的三角形是直角三角形?若存在求出点 P 的坐标; 若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com