
ЎҫМвДҝЎҝДіРЈОӘБЛҪвҫЕДкј¶С§ЙъөДКУБҰЗйҝцЈ¬Лж»ъійСщөчІйБЛІҝ·ЦҫЕДкј¶С§ЙъөДКУБҰЈ¬ТФПВКЗёщҫЭөчІйҪб№ы»жЦЖөДНіјЖНјұнөДТ»Іҝ·ЦЈ®
·ЦЧй | КУБҰ | ИЛКэ |
A | 3.95ЎЬxЎЬ4.25 | 2 |
B | 4.25ЈјxЎЬ4.55 | |
C | 4.55ЈјxЎЬ4.85 | 20 |
D | 4.85ЈјxЎЬ5.15 | |
E | 5.15ЈјxЎЬ5.45 | 3 |
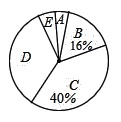
ёщҫЭТФЙПРЕПўЈ¬ҪвҙрПВБРОКМвЈә
ЈЁ1Ј©ФЪұ»өчІйС§ЙъЦРЈ¬КУБҰФЪ3.95ЎЬxЎЬ4.25·¶О§ДЪөДИЛКэОӘЎЎ ЎЎИЛЈ¬ФЪ4.25ЈјxЎЬ4.55·¶О§ДЪөДС§ЙъКэХјұ»өчІйөДС§ЙъКэөД°Щ·ЦұИОӘЎЎ ЎЎ%Ј®
ЈЁ2Ј©ұҫҙОөчІйөДСщұҫИЭБҝКЗЎЎ ЎЎЈ¬КУБҰФЪ4.85ЈјxЎЬ5.15·¶О§ДЪөДС§ЙъКэХјұ»өчІйС§ЙъКэөД°Щ·ЦұИКЗЎЎ ЎЎ%Ј®
ЈЁ3Ј©ұҫҙОөчІйЦРЈ¬КУБҰөДЦРО»КэВдФЪЎЎ ЧйЈ®
ЈЁ4Ј©ИфёГРЈҫЕДкј¶УР350ГыС§ЙъЈ¬№АјЖКУБҰі¬№э4.85өДС§ЙъКэЈ®
Ўҫҙр°ёЎҝЈЁ1Ј©2 16 Ј»ЈЁ2Ј© 50 34Ј»ЈЁ3Ј©CЈ»ЈЁ4Ј©140Ј»
ЎҫҪвОцЎҝ
ЈЁ1Ј©ёщҫЭұнёсҝЙЗуКУБҰФЪ3.95ЎЬxЎЬ4.25·¶О§ДЪөДИЛКэЈ¬ФЪ4.25ЈјxЎЬ4.55·¶О§ДЪөДС§ЙъКэХјұ»өчІйөДС§ЙъКэөД°Щ·ЦұИЈ»
ЈЁ2Ј©ёщҫЭCөДИЛКэУлХјұ»өчІйөДС§ЙъКэөД°Щ·ЦұИЈ¬ҝЙЗуұҫҙОөчІйөДСщұҫИЭБҝЈ¬ҪшТ»ІҪөГөҪAЎўEөД°Щ·ЦұИЈ¬ҙУ¶шЗуөГКУБҰФЪ4.85ЈјxЎЬ5.15·¶О§ДЪөДС§ЙъКэХјұ»өчІйС§ЙъКэөД°Щ·ЦұИЈ»
ЈЁ3Ј©ёщҫЭЦРО»КэөДЗу·ЁЈ¬Ҫ«КэҫЭҙУРЎөҪҙуЕЕБРЈ¬ХТЧоЦРјдБҪёцКэөДЖҪҫщКэјҙҝЙөГіцҙр°ёЈ»
ЈЁ4Ј©УГСщұҫЦРКУБҰі¬№э4.85өДС§ЙъКэИЛКэЈ¬јҙҝЙ№АјЖЧЬМеЦРКУБҰі¬№э4.85өДС§ЙъИЛКэЈ®
ЈЁ1Ј©ФЪұ»өчІйС§ЙъЦРЈ¬КУБҰФЪ3.95ЎЬxЎЬ4.25·¶О§ДЪөДИЛКэОӘ2ИЛЈ¬ФЪ4.25ЈјxЎЬ4.55·¶О§ДЪөДС§ЙъКэХјұ»өчІйөДС§ЙъКэөД°Щ·ЦұИОӘ16%Ј¬
№Кҙр°ёОӘЈә2Ј¬16Ј»
ЈЁ2Ј©20ЎВ40%=50Ј¬50ЎБ16%=8ЈЁИЛЈ©Ј¬1-16%-40%-ЈЁ2+3Ј©ЎВ50ЎБ100%=34%Ј¬
№КұҫҙОөчІйөДСщұҫИЭБҝКЗ50Ј¬КУБҰФЪ4.85ЈјxЎЬ5.15·¶О§ДЪөДС§ЙъКэХјұ»өчІйЙъКэөД°Щ·ЦұИКЗ34%Ј¬
№Кҙр°ёОӘЈә50Ј¬34Ј»
ЈЁ3Ј©Ҫ«КэҫЭҙУРЎөҪҙуЕЕБРЈ¬ЧоЦРјдБҪёцКэөД¶јФЪCЧйЈ¬№КұҫҙОөчІйЦРЈ¬КУБҰөДЦРО»КэВдФЪCЧйЈ¬
№Кҙр°ёОӘЈәCЈ»
ЈЁ4Ј©![]() ЎБ100%=6%Ј¬350ЎБЈЁ34%+6%Ј©=140ЈЁИЛЈ©Ј¬
ЎБ100%=6%Ј¬350ЎБЈЁ34%+6%Ј©=140ЈЁИЛЈ©Ј¬
№ККУБҰі¬№э4.85өДС§ЙъКэКЗ140Ј®



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
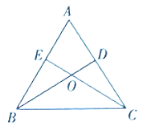
ЎҫМвДҝЎҝФЪЎчABCЦРЈ¬ABЈҪ13Ј¬ACЈҪ5Ј¬BCұЯЙПөДЦРПЯADЈҪ6Ј¬өгEФЪADөДСУіӨПЯЙПЈ¬ЗТEDЈҪADЈ®

ЈЁ1Ј©ЗуЦӨЈәBEЎОACЈ»
ЈЁ2Ј©ЗуЎПCADөДҙуРЎЈ»
ЈЁ3Ј©ЗуөгAөҪBCөДҫаАлЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝіӨ·ҪРОөДіӨәНҝн·ЦұрКЗaАеГЧЎўbАеГЧЈ¬Из№ыіӨ·ҪРОөДіӨәНҝнёчјхЙЩ2АеГЧЈ®
ЈЁ1Ј©РВіӨ·ҪРОөДГж»эұИФӯіӨ·ҪРОөДГж»эјхЙЩБЛ¶аЙЩЖҪ·ҪАеГЧЈҝ
ЈЁ2Ј©Из№ыјхЙЩөДГж»эЗЎәГөИУЪФӯГж»эөД![]() Ј¬КФИ·¶ЁЈЁa©Ғ6Ј©ЈЁb©Ғ6Ј©өДЦөЈ®
Ј¬КФИ·¶ЁЈЁa©Ғ6Ј©ЈЁb©Ғ6Ј©өДЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ИсҪЗ![]() өДБҪМхёЯ
өДБҪМхёЯ![]() Ўў
Ўў![]() ПаҪ»УЪөг
ПаҪ»УЪөг![]() Ј¬ЗТ
Ј¬ЗТ![]() Ј®
Ј®
ЈЁ1Ј©ЦӨГчЈә![]() Ј®
Ј®
ЈЁ2Ј©ЕР¶Пөг![]() КЗ·сФЪ
КЗ·сФЪ![]() өДҪЗЖҪ·ЦПЯЙПЈ¬ІўЛөГчАнУЙЈ®
өДҪЗЖҪ·ЦПЯЙПЈ¬ІўЛөГчАнУЙЈ®
ЈЁ3Ј©Б¬ҪУ![]() Ј¬
Ј¬![]() Ул
Ул![]() КЗ·сЖҪРРЈҝОӘКІГҙЈҝ
КЗ·сЖҪРРЈҝОӘКІГҙЈҝ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЈЁ1Ј©ИзНјIЈ¬ФЪ![]() ЦРЈ¬
ЦРЈ¬![]() .өг
.өг![]() ФЪ
ФЪ![]() НвЈ¬Б¬ҪУ
НвЈ¬Б¬ҪУ![]() Ј¬Чч
Ј¬Чч![]() Ј¬Ҫ»
Ј¬Ҫ»![]() УЪөг
УЪөг![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬Б¬ҪУ
Ј¬Б¬ҪУ![]() .Фт
.Фт![]() јдөДөИБҝ№ШПөКЗ______Ј»ЈЁІ»УГЦӨГчЈ©
јдөДөИБҝ№ШПөКЗ______Ј»ЈЁІ»УГЦӨГчЈ©
ЈЁ2Ј©ИзНјўтЈ¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬СУіӨ
Ј¬СУіӨ![]() Ҫ»
Ҫ»![]() УЪөг
УЪөг![]() Ј¬Рҙіц
Ј¬Рҙіц![]() јдөДөИБҝ№ШПөЈ¬ІўЦӨГчДгөДҪбВЫ.
јдөДөИБҝ№ШПөЈ¬ІўЦӨГчДгөДҪбВЫ.

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬Ҫ«ЎчABCИЖөгCЛіКұХлРэЧӘ90ЎгөГөҪЎчEDCЈ®ИфөгAЈ¬DЈ¬EФЪН¬Т»МхЦұПЯЙПЈ¬ЎПACB=20ЎгЈ¬ФтЎПADCөД¶ИКэКЗЈЁЎЎЎЎЈ©

A. 55Ўг B. 60Ўг C. 65Ўг D. 70Ўг
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
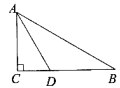
ЎҫМвДҝЎҝИзНј,ФЪRtЎчABCЦР,ЎПACB=90Ўг,ЎПB=30Ўг,ADОӘЎПCABөДҪЗЖҪ·ЦПЯ,ИфCD=3Ј¬ФтDB=____.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘOAЈ¬OBКЗЎСOөД°лҫ¶Ј¬ЗТOAЎНOBЈ¬ҙ№ЧгОӘOЈ¬PКЗЙдПЯOAЙПөДТ»өгЈЁөгAіэНвЈ©Ј¬ЦұПЯBPҪ»ЎСOУЪөгQЈ¬№эQЧчЎСOөДЗРПЯҪ»ЙдПЯOAУЪөгEЈ®
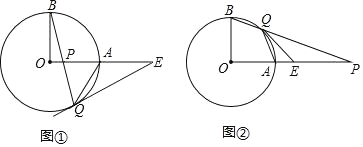
ЈЁ1Ј©ИзНјўЩЈ¬өгPФЪПЯ¶ОOAЙПЈ¬ИфЎПOBQ=15ЎгЈ¬ЗуЎПAQEөДҙуРЎЈ»
ЈЁ2Ј©ИзНјўЪЈ¬өгPФЪOAөДСУіӨПЯЙПЈ¬ИфЎПOBQ=65ЎгЈ¬ЗуЎПAQEөДҙуРЎЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДіМрЖ·өкУГ![]() Ј¬
Ј¬![]() БҪЦЦФӯБПЦЖЧчіЙјЧЎўТТБҪҝоМрЖ·ҪшРРПъКЫЈ¬ЦЖЧчГҝ·ЭМрЖ·өДФӯБПЛщРиУГБҝИзПВұнЛщКҫ.ёГөкЦЖЧчјЧҝоМрЖ·
БҪЦЦФӯБПЦЖЧчіЙјЧЎўТТБҪҝоМрЖ·ҪшРРПъКЫЈ¬ЦЖЧчГҝ·ЭМрЖ·өДФӯБПЛщРиУГБҝИзПВұнЛщКҫ.ёГөкЦЖЧчјЧҝоМрЖ·![]() ·ЭЈ¬ТТҝоМрЖ·
·ЭЈ¬ТТҝоМрЖ·![]() ·ЭЈ¬№ІУГИҘ
·ЭЈ¬№ІУГИҘ![]() ФӯБП2000ҝЛЈ®
ФӯБП2000ҝЛЈ®
ФӯБП ҝоКҪ |
ЈЁҝЛЈ© |
ЈЁҝЛЈ© |
јЧҝоМрЖ· | 30 | 15 |
ТТҝоМрЖ· | 10 | 20 |
ЈЁ1Ј©Зу![]() №ШУЪ
№ШУЪ![]() өДәҜКэұнҙпКҪЈ»
өДәҜКэұнҙпКҪЈ»
ЈЁ2Ј©ТСЦӘГҝ·ЭјЧМрЖ·өДАыИуОӘ5ФӘЈ¬Гҝ·ЭТТМрЖ·өДАыИуОӘ2ФӘ.јЩЙиБҪҝоМрЖ·ҫщДЬИ«ІҝВфіц.Иф»сөГЧЬАыИуІ»ЙЩУЪ360ФӘЈ¬ФтЦБЙЩТӘУГИҘ![]() ФӯБП¶аЙЩҝЛЈҝ
ФӯБП¶аЙЩҝЛЈҝ
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com