
【题目】如图,锐角![]() 的两条高
的两条高![]() 、
、![]() 相交于点
相交于点![]() ,且
,且![]() .
.
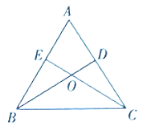
(1)证明:![]() .
.
(2)判断点![]() 是否在
是否在![]() 的角平分线上,并说明理由.
的角平分线上,并说明理由.
(3)连接![]() ,
,![]() 与
与![]() 是否平行?为什么?
是否平行?为什么?
【答案】(1)见解析(2)点O在∠BAC的角平分线上,理由见解析(3)平行,理由见解析
【解析】
(1)根据题意证明△BCE≌△CBD即可求解;
(2)由(1)得到△ABC为等腰三角形,连接AO并延长交BC于F,通过证△AOE≌△AOD,得到∠BAF=∠CAF,即点O在∠BAC的角平分线上.
(3)连接![]() ,根据等腰三角形三线合一即可求解.
,根据等腰三角形三线合一即可求解.
(1)∵锐角![]() 的两条高
的两条高![]() 、
、![]() 相交于点
相交于点![]() ,且
,且![]()
BC=CB,
∴△BCE≌△CBD(HL)
∴![]()
(2)解:点O在∠BAC的角平分线上.
理由:∵△BCE≌△CBD
∴∠EBC=∠DCB,BE=CD
∴△ABC为等腰三角形,
∴AB=AC,
则AB-BE=AC-CD
∴AE=AD
连接AO并延长交BC于F,
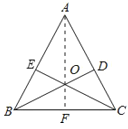
在Rt△AOE和Rt△AOD中,
![]()
∴Rt△AOE≌Rt△AOD.
∴∠BAF=∠CAF,
∴点O在∠BAC的角平分线上.
(3)平行,理由如下:
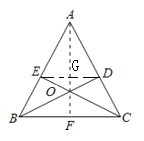
如图,连接![]() ,交AF于G点,
,交AF于G点,
∵AE=AD
∴△ADE为等腰三角形,
由(2)得到AF为∠BAC的角平分线
∴AG⊥DE,
又AF⊥BC,
∴DE∥BC.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两地之间的铁路交通设有特快列车和普通快车两种车次,某天一辆普通快车从甲地出发匀速向乙地行驶,同时另一辆特快列车从乙地出发匀速向甲地行驶,两车离甲地的路程S(千米)与行驶时间t(时)之间的函数关系如图所示.
(1)甲地到乙地的路成为________千米,普通快车到达乙地所用时间为_______小时.
(2)求特快列车离甲地的路程s与t之间的函数关系式.
(3)在甲、乙两地之间有一座铁路桥,特快列车到铁路桥后又行驶0.5小时与普通快车相遇,求甲地与铁路桥之间的路程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC是等腰直角三角形,BC=AB,A点在x负半轴上,直角顶点B在y轴上,点C在x轴上方.
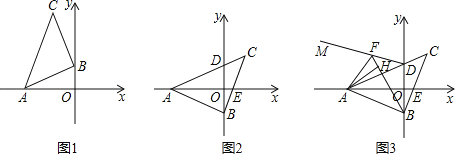
(1)如图1所示,若A的坐标是(﹣3,0),点B的坐标是(0,1),点C的坐标为 .
(2)如图2,若OA平分∠BAC,BC与x轴交于点E,若点C纵坐标为m,求AE的长.
(3)如图3,在(2)的条件下,点F在射线DM上,且∠ABF=∠ADF,AH⊥BF于点H,试探究BF、HFDF的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
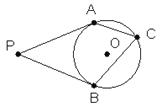
【题目】如图, PA、PB是⊙O的切线,切点为A、B,C是⊙O上一点(P与A、B不重合),若∠P=52°,则∠ACB=______________度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从宁海县到某市,可乘坐普通列车或高铁,已知高铁的行驶路程与普通列车的行驶路程之和是920千米,而普通列车的行驶路程是高铁的行驶路程的1.3倍.
(1)求普通列车的行驶路程;
(2)若高铁的平均速度(千米/时)是普通列车的平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求高铁的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解九年级学生的视力情况,随机抽样调查了部分九年级学生的视力,以下是根据调查结果绘制的统计图表的一部分.
分组 | 视力 | 人数 |
A | 3.95≤x≤4.25 | 2 |
B | 4.25<x≤4.55 | |
C | 4.55<x≤4.85 | 20 |
D | 4.85<x≤5.15 | |
E | 5.15<x≤5.45 | 3 |
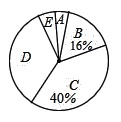
根据以上信息,解答下列问题:
(1)在被调查学生中,视力在3.95≤x≤4.25范围内的人数为 人,在4.25<x≤4.55范围内的学生数占被调查的学生数的百分比为 %.
(2)本次调查的样本容量是 ,视力在4.85<x≤5.15范围内的学生数占被调查学生数的百分比是 %.
(3)本次调查中,视力的中位数落在 组.
(4)若该校九年级有350名学生,估计视力超过4.85的学生数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆客车从甲地开住乙地,一辆出租车从乙地开往甲地,两车同时出发,两车距甲地的距离y(千米)与行驶时间式(小时)之间的函数图象如图所示,则下列说法中错误的是( )
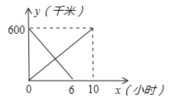
A. 客车比出租车晚4小时到达目的地B. 客车速度为60千米时,出租车速度为100千米/时
C. 两车出发后3.75小时相遇D. 两车相遇时客车距乙地还有225千米
查看答案和解析>>
科目:初中数学 来源: 题型:
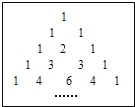
【题目】我国宋朝数学家杨辉在他的著作《详解九章算法》中提出如图,此表揭示了(a+b)n(n为非负整数)展开式的各项系数的规律,例如:(a+b)0=1,它只有一项,系数为1;(a+b)1=a+b,它有两项,系数分别为1,1;(a+b)2=a2+2ab+b2,它有三项,系数分别为1,2,1;(a+b)3=a3+3a2b+3ab2+b3,它有四项,系数分别为1,3,3,1;…;根据以上规律,(a+b)5展开式共有六项,系数分别为______,拓展应用:(a﹣b)4=_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com