
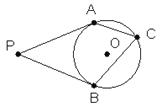
【题目】如图, PA、PB是⊙O的切线,切点为A、B,C是⊙O上一点(P与A、B不重合),若∠P=52°,则∠ACB=______________度.
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )

A.(﹣3,0) B.(﹣6,0) C.(![]() ,0) D.(
,0) D.(![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,回答问题:
两个含有二次根式的代数式相乘,如果它们的积不含有二次根式,我们就说这两个代数式互为有理化因式.例如:因为![]() ,
,![]() ,所
,所![]() 与
与![]() ,
,![]() 与
与![]() 互为有理化因式.
互为有理化因式.
(1)![]() 的有理化因式是 ;
的有理化因式是 ;
(2)这样,化简一个分母含有二次根式的式子时,采用分子、分母同乘以分母的有理化因式的方法就可以了,例如:
![]() ,
,

用上述方法对![]() 进行分母有理化.
进行分母有理化.
(3)利用所需知识判断:若![]() ,
,![]() ,则
,则![]() 的关系是 .
的关系是 .
(4)直接写结果:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长方形的长和宽分别是a厘米、b厘米,如果长方形的长和宽各减少2厘米.
(1)新长方形的面积比原长方形的面积减少了多少平方厘米?
(2)如果减少的面积恰好等于原面积的![]() ,试确定(a﹣6)(b﹣6)的值.
,试确定(a﹣6)(b﹣6)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
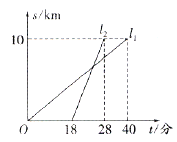
【题目】甲、乙两人以相同路线前往距离单位10km的培训中心参加学习,图中![]() ,
,![]() 分别表示甲、乙两人前往目的地所走的路程s(千米)随时间t(分)变化的函数图象,以下说法:①甲比乙提前12分到达;②甲的平均速度为15千米/时;③甲乙相遇时,乙走了6千米;④乙出发6分钟后追上甲.其中正确的有( )
分别表示甲、乙两人前往目的地所走的路程s(千米)随时间t(分)变化的函数图象,以下说法:①甲比乙提前12分到达;②甲的平均速度为15千米/时;③甲乙相遇时,乙走了6千米;④乙出发6分钟后追上甲.其中正确的有( )
A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图I,在![]() 中,
中,![]() .点
.点![]() 在
在![]() 外,连接
外,连接![]() ,作
,作![]() ,交
,交![]() 于点
于点![]() ,
,![]() ,
,![]() ,连接
,连接![]() .则
.则![]() 间的等量关系是______;(不用证明)
间的等量关系是______;(不用证明)
(2)如图Ⅱ,![]() ,
,![]() ,
,![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,写出
,写出![]() 间的等量关系,并证明你的结论.
间的等量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)探究新知:如图1,已知△ABC与△ABD的面积相等,试判断AB与CD的位置关系,并说明理由.

(2)结论应用:① 如图2,点M,N在反比例函数![]() (k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.试证明:MN∥EF.
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.试证明:MN∥EF.
② 若①中的其他条件不变,只改变点M,N的位置如图3所示,请判断 MN与EF是否平行?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com