
【题目】在△ABC中,AB=13,AC=5,BC边上的中线AD=6,点E在AD的延长线上,且ED=AD.

(1)求证:BE∥AC;
(2)求∠CAD的大小;
(3)求点A到BC的距离.
【答案】(1)证明见解析;(2)90°;(3)![]() .
.
【解析】
(1)先证明△ADC≌△EDB,可得∠CAD=∠BED,进而可得结论;
(2)由勾股定理逆定理可得△ABE是直角三角形,∠E=90°,进而可得∠CAD=∠E=90°;
(3)先由勾股定理求CD,再由AFCD=ACAD可求AF即可.
解:(1)证明:∵AD是△ABC的中线,
∴BD=CD,
在△ADC和△EDB中,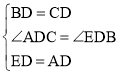 ,
,
∴△ADC≌△EDB(SAS),
∴∠CAD=∠BED,
∴BE∥AC.
(2)∵△ADC≌△EDB,
∴BE=AC=5,
在△ABE中,∵AB=13,BE=5,AE=2AD=12,
∴AE2+BE2=122+52=169,AB2=132=169,
∴AE2+BE2=AB2
∴∠E=90°,
∵BE∥AC,
∴∠CAD=∠E=90°;
(3)如图,过点A作AF⊥BC于F,
在Rt△ACD中,CD=![]() =
=![]() =
=![]() ,
,
∵AFCD=ACAD,
∴AF=![]() =
=![]() =
=![]() ,
,
即点A到BC的距离为![]() .
.


科目:初中数学 来源: 题型:
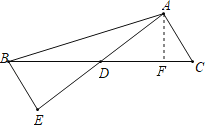
【题目】如图,已知矩形 OABC,以点 O 为坐标原点建立平面直角坐标系,其中 A(2,0), C(0,3),点 P 以每秒 1 个单位的速度从点 C 出发在射线 CO 上运动,连接 BP,作 BE⊥PB 交 x 轴于点 E,连接 PE 交 AB 于点 F,设运动时间为 t 秒.
(1)当 t=2 时,求点 E 的坐标;
(2)在运动的过程中,是否存在以 P、O、E 为顶点的三角形与△PCB 相似.若存在,请求出点 P 的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地之间的铁路交通设有特快列车和普通快车两种车次,某天一辆普通快车从甲地出发匀速向乙地行驶,同时另一辆特快列车从乙地出发匀速向甲地行驶,两车离甲地的路程S(千米)与行驶时间t(时)之间的函数关系如图所示.
(1)甲地到乙地的路成为________千米,普通快车到达乙地所用时间为_______小时.
(2)求特快列车离甲地的路程s与t之间的函数关系式.
(3)在甲、乙两地之间有一座铁路桥,特快列车到铁路桥后又行驶0.5小时与普通快车相遇,求甲地与铁路桥之间的路程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动课上,李老师让同学们试着用角尺平分 ![]() (如图所示),有两组.
(如图所示),有两组.
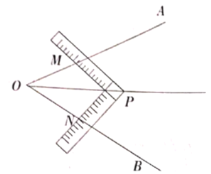
同学设计了如下方案:
方案①:将角尺的直角顶点![]() 介于射线
介于射线![]() 之间,移动角尺使角尺两边相同的刻度位于
之间,移动角尺使角尺两边相同的刻度位于![]() 上,且交点分别为
上,且交点分别为![]() ,即
,即![]() ,过角尺顶点
,过角尺顶点![]() 的射线
的射线![]() 就是
就是![]() 的平分线.
的平分线.
方案②:在边![]() 上分别截取
上分别截取![]() ,将角尺的直角顶点
,将角尺的直角顶点![]() 介于射线
介于射线![]() 之间,移动角尺使角尺两边相同的刻度与点
之间,移动角尺使角尺两边相同的刻度与点![]() 重合,即
重合,即![]() ,过角尺顶点
,过角尺顶点![]() 的射线
的射线![]() 就是
就是![]() 的平分线.请分别说明方案①与方案②是否可行?若可行,请证明; 若不可行,请说明理由.
的平分线.请分别说明方案①与方案②是否可行?若可行,请证明; 若不可行,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
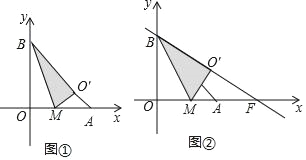
【题目】将一个直角三角形纸片ABO,放置在平面直角坐标系中,点A(2,0),点B(0,2),点O(0,0).点M为边OA上的一个动点(点M不与点O、A重合),沿着BM折叠该纸片,得顶点O的对应点O′.
(I)如图①,当点O′在边AB上时,求点O′的坐标;
(II)设直线BO′与x轴相交于点F.
①如图②,当BA平分∠MBF时,求点F的坐标;
②当OM=![]() 时,求点F的坐标(直接写出结果即可)
时,求点F的坐标(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解九年级学生的视力情况,随机抽样调查了部分九年级学生的视力,以下是根据调查结果绘制的统计图表的一部分.
分组 | 视力 | 人数 |
A | 3.95≤x≤4.25 | 2 |
B | 4.25<x≤4.55 | |
C | 4.55<x≤4.85 | 20 |
D | 4.85<x≤5.15 | |
E | 5.15<x≤5.45 | 3 |
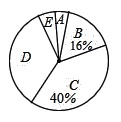
根据以上信息,解答下列问题:
(1)在被调查学生中,视力在3.95≤x≤4.25范围内的人数为 人,在4.25<x≤4.55范围内的学生数占被调查的学生数的百分比为 %.
(2)本次调查的样本容量是 ,视力在4.85<x≤5.15范围内的学生数占被调查学生数的百分比是 %.
(3)本次调查中,视力的中位数落在 组.
(4)若该校九年级有350名学生,估计视力超过4.85的学生数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com