
【题目】如图,已知矩形 OABC,以点 O 为坐标原点建立平面直角坐标系,其中 A(2,0), C(0,3),点 P 以每秒 1 个单位的速度从点 C 出发在射线 CO 上运动,连接 BP,作 BE⊥PB 交 x 轴于点 E,连接 PE 交 AB 于点 F,设运动时间为 t 秒.
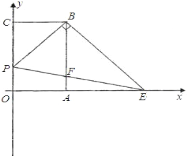
(1)当 t=2 时,求点 E 的坐标;
(2)在运动的过程中,是否存在以 P、O、E 为顶点的三角形与△PCB 相似.若存在,请求出点 P 的坐标;若不存在,请说明理由.
【答案】(1)(5,0);(2)存在.
【解析】
(1)本题需先求出AB=AE,再求出DE=5,即可求出点E的坐标.
(2)本题需先求出CP=CB=2,即可求出t的值.(3)本题需先证出△BCP~△BAE,求出
AE= t,再证出△POE~△PCB,求出的t值,再求出OP的长,即可求出P的坐标.
解:(1)当 t=2 时,PC=2,∵BC=2,∴PC=BC,∴∠PBC=45°,∴∠BAE=90°,
∴∠AEB=45°,∴AB=AE=3,OE=5,∴点 E 的坐标是(5,0);
(2)存在,
∵∠ABE+∠ABP=90°
∠PBC+∠ABP=90°
∴∠ABE=∠PBC
∵∠BAE=∠BCP=90°
∴△POE![]() △BAE
△BAE
∴![]() =
=![]()
∴![]() =
=![]()
∴AE=![]() t
t
∵若△POE![]() △PCB
△PCB
∴![]()
∴![]() =
=![]()
![]() ,
,![]() (舍去)
(舍去)
∴P的坐标为(0,![]() ).
).


科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,![]() .
.
(1)若![]() ,函数图象与
,函数图象与![]() 轴只有一个交点,求
轴只有一个交点,求![]() 的值;
的值;
(2)若![]() ,
,![]() ,设
,设![]() 点的横坐标为
点的横坐标为![]() ,求证:
,求证:![]() ;
;
(3)若![]() ,
,![]() ,问是否存在实数
,问是否存在实数![]() ,使得
,使得![]() 在
在![]() 时,
时,![]() 随
随![]() 的增大而增大?若存在,求
的增大而增大?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地高速铁路建设成功.试运行期间,一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车同时出发.设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示y与x之间的函数关系,根据图象分析出以下信息:①甲乙两地相距1000千米;②动车从甲地到乙地共需要4个小时;③![]() 表示的实际意义是动车的速度;④普通列车的速度是
表示的实际意义是动车的速度;④普通列车的速度是![]() 千米/小时;⑤动车到达乙地停留2小时后返回甲地,在普通列车出发后7.5小时和动车再次相遇.以上信息正确的是( )
千米/小时;⑤动车到达乙地停留2小时后返回甲地,在普通列车出发后7.5小时和动车再次相遇.以上信息正确的是( )
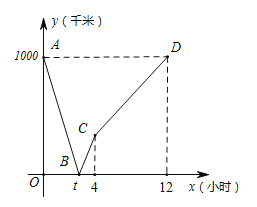
A.①②④B.①③④⑤C.①②④⑤D.②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,长方形OABC,点A,C分别在y轴,x轴的正半轴上,OA=6,OC=3.∠DOE=45°,OD,OE分别交BC,AB于点D,E,且CD=2,则点E坐标为_____.
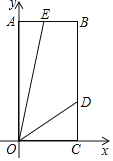
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,直线AB:y=kx+3(k≠0)交x轴于点A(4,0),交y轴正半轴于点B,过点C(0,2)作y轴的垂线CD交AB于点E,点P从E出发,沿着射线ED向右运动,设PE=n.
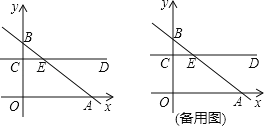
(1)求直线AB的表达式;
(2)当△ABP为等腰三角形时,求n的值;
(3)若以点P为直角顶点,PB为直角边在直线CD的上方作等腰Rt△BPM,试问随着点P的运动,点M是否也在直线上运动?如果在直线上运动,求出该直线的解析式;如果不在直线上运动,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
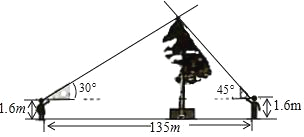
【题目】清明节假期,小红和小阳随爸妈去旅游,他们在景点看到一棵古松树,小红惊讶的说:“呀!这棵树真高!有60多米.”小阳却不以为然:“60多米?我看没有.”两个人争论不休,爸爸笑着说:“别争了,正好我带了一副三角板,用你们学过的知识量一量、算一算,看谁说的对吧!”
小红和小阳进行了以下测量:如图所示,小红和小阳分别在树的东西两侧同一地平线上,他们用手平托三角板,保持三角板的一条直角边与地平面平行,然后前后移动各自位置,使目光沿着三角板的斜边正好经过树的最高点,这时,测得小红和小阳之间的距离为135米,他们的眼睛到地面的距离都是1.6米.通过计算说明小红和小阳谁的说法正确(计算结果精确到0.1)(参考数据![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )

A.(﹣3,0) B.(﹣6,0) C.(![]() ,0) D.(
,0) D.(![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=13,AC=5,BC边上的中线AD=6,点E在AD的延长线上,且ED=AD.

(1)求证:BE∥AC;
(2)求∠CAD的大小;
(3)求点A到BC的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长方形的长和宽分别是a厘米、b厘米,如果长方形的长和宽各减少2厘米.
(1)新长方形的面积比原长方形的面积减少了多少平方厘米?
(2)如果减少的面积恰好等于原面积的![]() ,试确定(a﹣6)(b﹣6)的值.
,试确定(a﹣6)(b﹣6)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com