
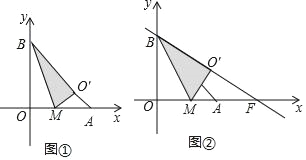
【题目】将一个直角三角形纸片ABO,放置在平面直角坐标系中,点A(2,0),点B(0,2),点O(0,0).点M为边OA上的一个动点(点M不与点O、A重合),沿着BM折叠该纸片,得顶点O的对应点O′.
(I)如图①,当点O′在边AB上时,求点O′的坐标;
(II)设直线BO′与x轴相交于点F.
①如图②,当BA平分∠MBF时,求点F的坐标;
②当OM=![]() 时,求点F的坐标(直接写出结果即可)
时,求点F的坐标(直接写出结果即可)
【答案】(Ⅰ)O'(![]() ,2﹣
,2﹣![]() );(Ⅱ)①F(2
);(Ⅱ)①F(2![]() ,0);②F(
,0);②F(![]() ,0)
,0)
【解析】
(I) 过点O'作O'H⊥y轴于H,由折叠可知,BO'=BO=2,∠BO'H=∠BAO=45°,利用特殊角的三角函数值求出BH、O'H,从而得到O'的坐标;
(II) ①由BA平分∠MBF时,得到∠OBF=60,利用特殊角的三角函数值求出OF,即可得到点F的坐标;②先说明△FO'M∽△FOB,从而![]() =
=![]() ,设F(a,0),利用勾股定理,用含a式子表示O'F,代入
,设F(a,0),利用勾股定理,用含a式子表示O'F,代入![]() =
=![]() ,求出a,从而得到点F的坐标.
,求出a,从而得到点F的坐标.
解:(I)如图①,过点O'作O'H⊥y轴于H,
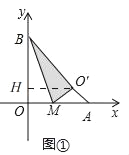
由折叠知,△BMO≌△BMO',
∴BO'=BO=2,
∵O'H∥OA,
∴∠BO'H=∠BAO=45°,
在Rt△BO'H中,O'H=BO'cos∠BO'H=![]() ,
,
∴BH=O'H=![]() ,
,
∴OH=OB﹣BH=2﹣![]() ,
,
∴O'(![]() ,2﹣
,2﹣![]() );
);
(II)①∵BA平分∠MBF,
∴∠ABO=3∠MBA=45°,
∴∠ABF=∠MBA=15°,
∴∠OBF=∠ABO+∠ABF=60°,
在Rt△BOF中,OF=OBtan60=2![]() ,
,
∴F(2![]() ,0);
,0);
②由折叠知,O'M=OM=![]() ,O'B=OB=2,∠MO'F=90°=∠FOB,
,O'B=OB=2,∠MO'F=90°=∠FOB,
∵∠FO'M=∠FOB,
∴△FO'M∽△FOB,
∴![]() =
=![]() ,
,
设F(a,0)(a>0),
∴OF=a,
在Rt△BOF中,BF=![]() ,
,
∴O'F=![]() ﹣2,
﹣2,
∴![]() ,
,
∴a=0(舍)或a=![]() ,
,
F(![]() ,0).
,0).
故答案为:(I)O'(![]() ,2﹣
,2﹣![]() );(II)①F(2
);(II)①F(2![]() ,0);②F(
,0);②F(![]() ,0)
,0)


科目:初中数学 来源: 题型:
【题目】甲、乙两地高速铁路建设成功.试运行期间,一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车同时出发.设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示y与x之间的函数关系,根据图象分析出以下信息:①甲乙两地相距1000千米;②动车从甲地到乙地共需要4个小时;③![]() 表示的实际意义是动车的速度;④普通列车的速度是
表示的实际意义是动车的速度;④普通列车的速度是![]() 千米/小时;⑤动车到达乙地停留2小时后返回甲地,在普通列车出发后7.5小时和动车再次相遇.以上信息正确的是( )
千米/小时;⑤动车到达乙地停留2小时后返回甲地,在普通列车出发后7.5小时和动车再次相遇.以上信息正确的是( )
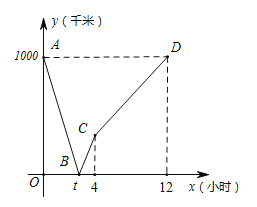
A.①②④B.①③④⑤C.①②④⑤D.②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )

A.(﹣3,0) B.(﹣6,0) C.(![]() ,0) D.(
,0) D.(![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=13,AC=5,BC边上的中线AD=6,点E在AD的延长线上,且ED=AD.

(1)求证:BE∥AC;
(2)求∠CAD的大小;
(3)求点A到BC的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
[问题]如图1,在![]() 中,
中,![]() ,过点
,过点![]() 作直线
作直线![]() 平行于
平行于![]() ,点
,点![]() 在直线
在直线![]() 上移动,角的一边DE始终经过点
上移动,角的一边DE始终经过点![]() ,另一边
,另一边![]() 与
与![]() 交于点
交于点![]() ,研究
,研究![]() 和
和![]() 的数量关系.
的数量关系.
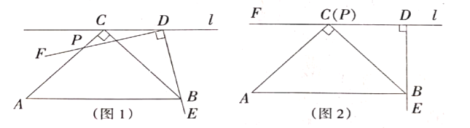
[探究发现]
(1)如图2,某数学学习小组运用“从特殊到一般”的数学思想,发现当点![]() 移动到使点
移动到使点![]() 与点
与点![]() 重合时,很容易就可以得到
重合时,很容易就可以得到![]() 请写出证明过程;
请写出证明过程;
[数学思考]
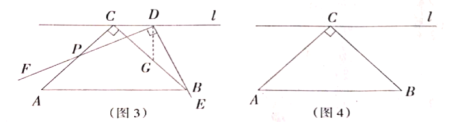
(2)如图3,若点![]() 是
是![]() 上的任意一点(不含端点
上的任意一点(不含端点![]() ),受(1)的启发,另一个学习小组过点
),受(1)的启发,另一个学习小组过点![]() ,
,![]() 交
交![]() 于点
于点![]() ,就可以证明
,就可以证明![]() ,请完成证明过程;
,请完成证明过程;
[拓展引申]
(3)若点![]() 是
是![]() 延长线上的任意一点,在图(4)中补充完整图形,并判断结论是否仍然成立.
延长线上的任意一点,在图(4)中补充完整图形,并判断结论是否仍然成立.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在△ABC边延长线上,点O是边AC上一个动点,过O作直线EF∥BC,交∠BCA的平分线于点F,交∠BCA的外角平分线于E.当点O在线段AC上移动(不与点A,C重合)时,下列结论不一定成立的是( )
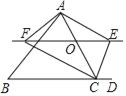
A. 2∠ACE=∠BAC+∠B B. EF=2OC C. ∠FCE=90° D. 四边形AFCE是矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,回答问题:
两个含有二次根式的代数式相乘,如果它们的积不含有二次根式,我们就说这两个代数式互为有理化因式.例如:因为![]() ,
,![]() ,所
,所![]() 与
与![]() ,
,![]() 与
与![]() 互为有理化因式.
互为有理化因式.
(1)![]() 的有理化因式是 ;
的有理化因式是 ;
(2)这样,化简一个分母含有二次根式的式子时,采用分子、分母同乘以分母的有理化因式的方法就可以了,例如:
![]() ,
,

用上述方法对![]() 进行分母有理化.
进行分母有理化.
(3)利用所需知识判断:若![]() ,
,![]() ,则
,则![]() 的关系是 .
的关系是 .
(4)直接写结果:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长方形的长和宽分别是a厘米、b厘米,如果长方形的长和宽各减少2厘米.
(1)新长方形的面积比原长方形的面积减少了多少平方厘米?
(2)如果减少的面积恰好等于原面积的![]() ,试确定(a﹣6)(b﹣6)的值.
,试确定(a﹣6)(b﹣6)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com