
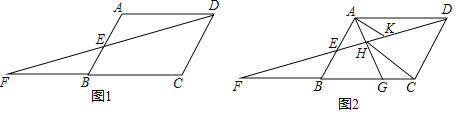
【题目】已知,如图1,在ABCD中,点E是AB中点,连接DE并延长,交CB的延长线于点F.
(1)求证:△ADE≌△BFE;
(2)如图2,点G是边BC上任意一点(点G不与点B、C重合),连接AG交DF于点H,连接HC,过点A作AK∥HC,交DF于点K.
①求证:HC=2AK;
②当点G是边BC中点时,恰有HD=nHK(n为正整数),求n的值.
【答案】(1)证明见解析;(2)证明见解析;(3)n=4.
【解析】
此题涉及的知识点是两三角形全等的判定,平行四边形的性质点的综合应用,解题时先根据已知条件证明△ADE≌△BFE,再根据两三角形相似的判定,等量代换得出边的大小关系
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADE=∠BFE,∠A=∠FBE,
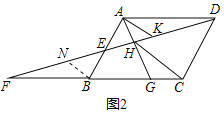
在△ADE和△BFE中,
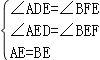 ,
,
∴△ADE≌△BFE;
(2)如图2,作BN∥HC交EF于N,
∵△ADE≌△BFE,
∴BF=AD=BC,
∴BN=![]() HC,
HC,
由(1)的方法可知,△AEK≌△BEN,
∴AK=BN,
∴HC=2AK;
(3)如图3,作GM∥DF交HC于M,
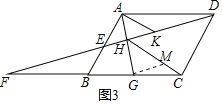
∵点G是边BC中点,
∴CG=![]() CF,
CF,
∵GM∥DF,
∴△CMG∽△CHF,
∴![]() =
=![]() =
=![]() ,
,
∵AD∥FC,
∴△AHD∽△GHF,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵AK∥HC,GM∥DF,
∴△AHK∽△HGM,
∴![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,即HD=4HK,
,即HD=4HK,
∴n=4.


科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,∠CAB的角平分线AD交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)若∠CAB=60°,DE=3![]() ,求AC的长.
,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
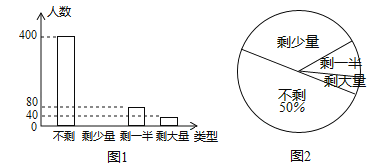
【题目】某企业工会开展“一周工作量完成情况”调查活动,随机调查了部分员工一周的工作量剩余情况,并将调查结果统计后绘制成如图 1 和图 2 所示的不完整统计图 .
(1) 被调查员工的人数为 人:
(2) 把条形统计图补充完整;
(3) 若该企业有员工 10000 人,请估计该企业某周的工作量完成情况为“剩少量”的员工有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的对称轴是x=﹣1,且过点(![]() ,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a+4c=10b;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有错误的结论有( )个.
,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a+4c=10b;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有错误的结论有( )个.
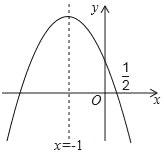
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )
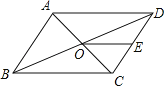
A. 15 B. 18 C. 21 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将一个量角器与一张等边三角形(△ABC)纸片放置成轴对称图形,CD⊥AB,垂足为D,半圆(量角器)的圆心与点D重合,此时,测得顶点C到量角器最高点的距离CE=2cm,将量角器沿DC方向平移1cm,半圆(量角器)恰与△ABC的边AC,BC相切,如图2,则AB的长为__________cm.
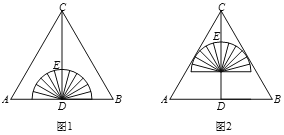
查看答案和解析>>
科目:初中数学 来源: 题型:
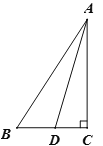
【题目】如图,Rt△ ABC中,∠ACB=90°,AD平分∠BAC, 作AD的垂直平分线EF交AD于点E,交BC的延长线于点F,交AB于点G,交AC于点H.
(1)依题意补全图形;
(2)求证:∠BAD=∠BFG;
(3)试猜想AB,FB和FD之间的数量关系并进行证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
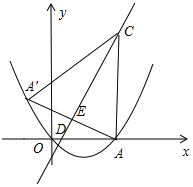
【题目】如图所示,抛物线y=ax2-![]() x+c经过原点O与点A(6,0)两点,过点A作AC⊥x轴,交直线y=2x-2于点C,且直线y=2x-2与x轴交于点D.
x+c经过原点O与点A(6,0)两点,过点A作AC⊥x轴,交直线y=2x-2于点C,且直线y=2x-2与x轴交于点D.
(1)求抛物线的解析式,并求出点C和点D的坐标;
(2)求点A关于直线y=2x-2的对称点A′的坐标,并判断点A′是否在抛物线上,并说明理由;
(3)点P(x,y)是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点Q,设线段PQ的长为l,求l与x的函数关系式及l的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com