
【题目】如图,AB为⊙O的直径,C为⊙O上一点,∠CAB的角平分线AD交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)若∠CAB=60°,DE=3![]() ,求AC的长.
,求AC的长.

【答案】(1)见解析;(2)6.
【解析】
(1)连接OD,由已知得∠ODA=∠OAD=∠DAC,从而OD∥AE,由此能证明DE是圆O的切线.
(2)连接BD,则∠ADB=90°,由角平分线的定义可求∠CAD=∠DAB=30°,尽而可求DE、AD、AB的长,连接OC,可证AC=OA=OC=6.
证明:(1)连接OD,如图,
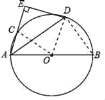
∵OA=OD,
∴∠OAD=∠ODA,
∵AD平分∠CAB,
∴∠CAD=∠OAD,
∴∠CAD=∠ODA,
∴OD∥AC,
∵DE⊥AC,
∴DE⊥OD,
∴DE是⊙O的切线;
(2)连接BD,则∠ADB=90°,
∵∠CAB=60°,AD平分∠CAB,
∴∠CAD=∠DAB=30°,
∵DE=3![]() ,
,
∴AD=6![]() ,
,
∴AB=12,
连接OC,则OC=OA=6,
∵∠CAB=60°,
∴AC=OA=OC=6.


科目:初中数学 来源: 题型:
【题目】随着几何部分的学习,小鹏对几何产生了浓厚的兴趣,他最喜欢利用手中的工具画图了![]() 如图,作一个
如图,作一个![]() ,以O为圆心任意长为半径画弧分别交OA,OB于点C和点D,将一副三角板如图所示摆放,两个直角三角板的直角顶点分别落在点C和点D,直角边中分别有一边与角的两边重合,另两条直角边相交于点P,连接
,以O为圆心任意长为半径画弧分别交OA,OB于点C和点D,将一副三角板如图所示摆放,两个直角三角板的直角顶点分别落在点C和点D,直角边中分别有一边与角的两边重合,另两条直角边相交于点P,连接![]() 小鹏通过观察和推理,得出结论:OP平分
小鹏通过观察和推理,得出结论:OP平分![]() .
.
你同意小鹏的观点吗?如果你同意小鹏的观点,试结合题意写出已知和求证,并证明.
已知:![]() 中,______
中,______![]() ______,______
______,______![]() ______,______
______,______![]() ______.
______.
求证:OP平分![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
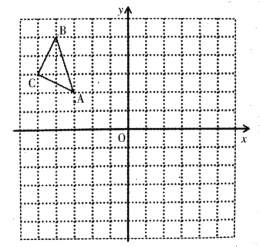
【题目】如图,在平面直角坐标系中,A(﹣1,5)、B(﹣1,0)、C(﹣4,3).

(1)请画出△ABC关于y轴对称的△DEF(其中D、E、F分别是A、B、C的对应点).
(2)直接写出(1)中F点的坐标为 .
(3)若直线l经过点(0,﹣2)且与x轴平行,则点C关于直线l的对称点的坐标为 .
(4)在y轴上存在一点P,使PC﹣PB最大,则点P的坐标为 .
(5)第一象限有一点M(4,2),在x轴上找一点Q使CQ+MQ最短,画出最短路径,保留作图痕迹.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2﹣9ax+18a的图象与x轴交于A,B两点(A在B的左侧),图象的顶点为C,直线AC交y轴于点D.
(1)连接BD,若∠BDO=∠CAB,求这个二次函数的表达式;
(2)是否存在以原点O为对称轴的矩形CDEF?若存在,求出这个二次函数的表达式,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(-3,2).请按要求分别完成下列各小题:
(1)把△ABC向下平移4个单位得到△A1B1C1,画出△A1B1C1,点A1的坐标是___.
(2)画出△ABC关于y轴对称的△A2B2C2,则点C2的坐标是 ;
(3)△ABC的面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
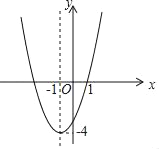
【题目】已知二次函数的图象如图所示.
(1)求这个二次函数的表达式;
(2)将该二次函数图象向上平移 个单位长度后恰好过点(﹣2,0);
(3)观察图象,当﹣2<x<1时,y的取值范围为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是甲、乙两家运输公司规定每位旅客携带行李的费用与所带行李质量之间的关系图.
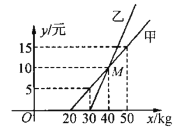
(1)由图可知,行李质量只要不超过______kg,甲公司就可免费携带,如果超过了规定的质量,则每超过1 kg要付运费_______元;
(2)若设旅客携带的行李质量为x(kg),所付的行李费是y(元),请分别写出y甲与y乙(元)随x(kg)之间变化的关系式;
(3)若你准备携带45 kg的行李出行,在甲、乙两家公司中你会选择哪一家?应付行李费多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com