
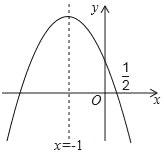
【题目】如图,抛物线y=ax2+bx+c的对称轴是x=﹣1,且过点(![]() ,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a+4c=10b;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有错误的结论有( )个.
,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a+4c=10b;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有错误的结论有( )个.
A. 1 B. 2 C. 3 D. 4
【答案】B
【解析】
根据抛物线的开口方向、对称轴、与y轴的交点判定系数符号,及运用一些特殊点解答问题.
由抛物线的开口向下可得:a<0,
根据抛物线的对称轴在y轴左边可得:a,b同号,所以b<0,
根据抛物线与y轴的交点在正半轴可得:c>0,
∴abc>0,故①正确;
直线x=﹣1是抛物线y=ax2+bx+c(a≠0)的对称轴,所以﹣![]() =﹣1,可得b=2a,
=﹣1,可得b=2a,
a﹣2b+4c=a﹣4a+4c=﹣3a+4c,
∵a<0,
∴﹣3a>0,
∴﹣3a+4c>0,
即a﹣2b+4c>0,故②错误;
∵抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点(![]() ,0),
,0),
∴抛物线与x轴的另一个交点坐标为(﹣![]() ,0),
,0),
当x=﹣![]() 时,y=0,即a(﹣
时,y=0,即a(﹣![]() )2+b×(﹣
)2+b×(﹣![]() )+c=0,
)+c=0,
整理得:25a﹣10b+4c=0,故③正确;
∵b=2a,a+b+c<0,
∴![]() b+b+c<0,
b+b+c<0,
即3b+2c<0,故④错误;
∵x=﹣1时,函数值最大,
∴a﹣b+c>m2a﹣mb+c(m≠﹣1),
∴a﹣b>m(am﹣b),所以⑤正确;
故选:B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣![]() x2+bx+c经过点(1,0),(0,
x2+bx+c经过点(1,0),(0,![]() ).
).
(1)求该抛物线的函数表达式;
(2)将抛物线y=﹣![]() x2+bx+c平移,使其顶点恰好落在原点,请写出一种平移的方法及平移后的函数表达式.
x2+bx+c平移,使其顶点恰好落在原点,请写出一种平移的方法及平移后的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b2﹣4ax>0;②2a+b>0;③abc<0;④4a﹣2b+c<0;⑤a+b+c>0.其中正确的个数是( )
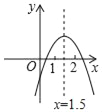
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动小组的同学为测量旗杆高度,先制定了如下测量方案,使用工具是测角仪和皮尺,请帮助组长林平完成方案内容,用含a,b,α的代数式表示旗杆AB的高度.
数学活动方案
活动时间:2018年4月2日 活动地点:学校操场 填表人:林平
课题 | 测量学校旗杆的高度 | ||
活动目的 | 运用所学数学知识及方法解决实际问题 | ||
方案示意图 |
| 测量步骤 | (1)用什么测得∠ADE=α; (2)用什么测得BC=a米,CD=b米. |
(3)计算过程 | |||
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在四张背面完全相同的纸牌的正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀后摸出一张,不放回,再摸出一张
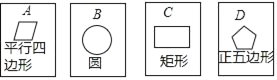
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A、B、C、D表示);
(2)求摸出的两张纸牌牌面上所画几何图形既是轴对称图形又是中心对称图形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
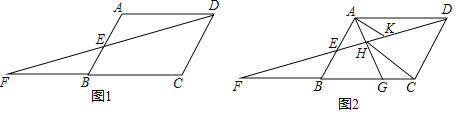
【题目】已知,如图1,在ABCD中,点E是AB中点,连接DE并延长,交CB的延长线于点F.
(1)求证:△ADE≌△BFE;
(2)如图2,点G是边BC上任意一点(点G不与点B、C重合),连接AG交DF于点H,连接HC,过点A作AK∥HC,交DF于点K.
①求证:HC=2AK;
②当点G是边BC中点时,恰有HD=nHK(n为正整数),求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
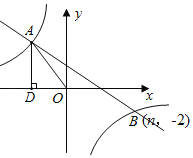
【题目】如图所示,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象交于第二、四象限A、B两点,过点A作AD⊥x轴于D,AD=4,sin∠AOD=
(m≠0)的图象交于第二、四象限A、B两点,过点A作AD⊥x轴于D,AD=4,sin∠AOD=![]() ,且点B的坐标为(n,-2).
,且点B的坐标为(n,-2).
(1)求一次函数与反比例函数的解析式;
(2)E是y轴上一点,且△AOE是等腰三角形,请直接写出所有符合条件的E点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年(1)班的体育课上,小明、小强和小华三人在学习训练足球,足球从一人传到另一人就记为踢一次.
(1)如果从小强开始踢,经过两次踢球后,足球踢到了小明处的概率是多少?请用数状图或列表法说明.
(2)如果踢三次,球踢到了小明处的可能性最小,应从谁开始踢?(直接写出结论)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com