
【题目】已知抛物线y=﹣![]() x2+bx+c经过点(1,0),(0,
x2+bx+c经过点(1,0),(0,![]() ).
).
(1)求该抛物线的函数表达式;
(2)将抛物线y=﹣![]() x2+bx+c平移,使其顶点恰好落在原点,请写出一种平移的方法及平移后的函数表达式.
x2+bx+c平移,使其顶点恰好落在原点,请写出一种平移的方法及平移后的函数表达式.
【答案】(1)抛物线解析式为y=﹣![]() x2﹣x+
x2﹣x+![]() ;(2)抛物线向右平移一个单位,向下平移2个单位,解析式变为y=﹣
;(2)抛物线向右平移一个单位,向下平移2个单位,解析式变为y=﹣![]() x2
x2
【解析】
(1)将(1,0)和(0,号)代入抛物线解析式得到-个关于b和c的二元-次方程组,解之即可得抛物线解析式.
(2)将(1)中求得的解析式配方得其顶点坐标为(-1,2),故使其顶点恰好落在原点的一种平移方法:先向右平移1个单位长度,再向下平移2个单位长度;从而可得平移后的函数表达式.
(1)把(1,0),(0,![]() )代入抛物线解析式得:
)代入抛物线解析式得: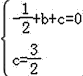 ,
,
解得:![]() ,
,
则抛物线解析式为y=﹣![]() x2﹣x+
x2﹣x+![]() ;
;
(2)抛物线解析式为y=﹣![]() x2﹣x+
x2﹣x+![]() =﹣
=﹣![]() (x+1)2+2,
(x+1)2+2,
将抛物线向右平移一个单位,向下平移2个单位,解析式变为y=﹣![]() x2.
x2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在直角坐标系中,函数y=![]() (x>0,k为常数)的图象经过A(4,1),点B(a,b)(0<a<4)是双曲线上的一动点,过A作AC⊥y轴于C,点D是坐标系中的另一点.若以A.B.C.D为顶点的平行四边形的面积为12,那么对角线长度的最大值为_____.
(x>0,k为常数)的图象经过A(4,1),点B(a,b)(0<a<4)是双曲线上的一动点,过A作AC⊥y轴于C,点D是坐标系中的另一点.若以A.B.C.D为顶点的平行四边形的面积为12,那么对角线长度的最大值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;
(2)求∠FAE的度数;
(3)求证:CD=2BF+DE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
数学活动课上,老师出了一道作图问题:“如图,已知直线l和直线l外一点P.用直尺和圆规作直线PQ,使PQ⊥l于点Q.”

小艾的作法如下:
(1)在直线l上任取点A,以A为圆心,AP长为半径画弧.
(2)在直线l上任取点B,以B为圆心,BP长为半径画弧.
(3)两弧分别交于点P和点M
(4)连接PM,与直线l交于点Q,直线PQ即为所求.
老师表扬了小艾的作法是对的.
请回答:小艾这样作图的依据是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD,AB=AC,E、F分别是BC,AD的中点,连接AE、CF.
(1)求证:四边形AECF是矩形;
(2)若AB=2,求菱形的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名队员参加射击训练,每人射击10次,成绩分别如下:

根据以上信息,整理分析数据如下:
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 | a | 7 | 7 | 1.2 |
乙 | 7 | b | 8 | c |
(1)a=_____;b=_____;c=_____;
(2)填空:(填“甲”或“乙”).
①从平均数和中位数的角度来比较,成绩较好的是_____;
②从平均数和众数的角度来比较,成绩较好的是_____;
③成绩相对较稳定的是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,E为CD中点,连接AE并延长AE交BC的延长线于点F.
(1)求证:CF=AD.
(2)若AD=3,AB=8,当BC为多少时,点B在线段AF的垂直平分线上,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县实施“村村通”工程中,决定在A、B两村之间修筑一条公路,甲、乙两个工程队分别从A、B两村同时开始修筑,施工期间,乙队因另有任务提前离开,余下的任务由甲队单独完成,直到道路修通,下图是甲、乙两个工程队修道路长度y(米)与修筑时间x(天)之间的函数图象,请根据图象所提供的信息,解答下列问题:
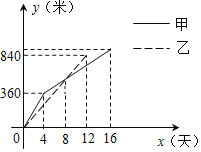
(1)写出乙工程队修道路的长度y与修筑时间x之间的函数关系式:_____;
(2)甲工程队前8天所修公路为_____米,该公路的总长度为_____米;
(3)若乙工程队不提前离开,则两队只需_____天就能完成任务;
(4)甲、乙两工程队第_____天时所修道路的长度相差80米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com