
【题目】如图,在梯形ABCD中,AD∥BC,E为CD中点,连接AE并延长AE交BC的延长线于点F.
(1)求证:CF=AD.
(2)若AD=3,AB=8,当BC为多少时,点B在线段AF的垂直平分线上,为什么?

【答案】(1)见解析;(2)当BC=5时,点B在线段AF的垂直平分线上,理由见解析.
【解析】
(1)根据平行线的性质可得∠D=∠ECF,利用ASA可证明△FEC≌△AED,即可证明CF=AD;
(2)若点B在线段AF的垂直平分线上,则应有AB=BF,根据AB=8,CF=AD=3,BC=BF﹣CF即可求出BC的长.
(1)∵AD∥BC,
∴∠D=∠DCF,
在△FEC与△AED中,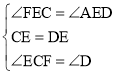 ,
,
∴△FEC≌△AED(ASA),
∴CF=AD.
(2)当BC=5时,点B在线段AF的垂直平分线上,
理由:∵点B在AF的垂直平分线上,
∴AB=BF,
∴AB=BC+CF,
∵AD=CF,
∴AB=BC+AD,
∵BC=5,AD=3,AB=8,
∴BC=AB-AD=5,
∴当BC=5时,点B在线段AF的垂直平分线上.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图,已知直角坐标系中一条圆弧经过正方形网格的格点![]() 、
、![]() 、
、![]() .若
.若![]() 点的坐标为
点的坐标为![]() ,
,![]() 点的坐标为
点的坐标为![]() ,
,
![]() 圆弧所在圆的圆心
圆弧所在圆的圆心![]() 点的坐标为________
点的坐标为________
![]() 点
点![]() 是否在经过点
是否在经过点![]() 、
、![]() 、
、![]() 三点的抛物线上;
三点的抛物线上;
![]() 在
在![]() 的条件下,求证:直线
的条件下,求证:直线![]() 是
是![]() 的切线.
的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣![]() x2+bx+c经过点(1,0),(0,
x2+bx+c经过点(1,0),(0,![]() ).
).
(1)求该抛物线的函数表达式;
(2)将抛物线y=﹣![]() x2+bx+c平移,使其顶点恰好落在原点,请写出一种平移的方法及平移后的函数表达式.
x2+bx+c平移,使其顶点恰好落在原点,请写出一种平移的方法及平移后的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,已知三角形ABC的边AB是⊙O的切线,切点为B.AC经过圆心O并与圆相交于点D、C,过C作直线CE丄AB,交AB的延长线于点E.

(1)求证:CB平分∠ACE;
(2)若BE=3,CE=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.掷一枚均匀的骰子,骰子停止转动后,6点朝上是必然事件
B.甲、乙两人在相同条件下各射击10次,他们的成绩平均数相同,方差分别是![]() ,
,![]() ,则甲的射击成绩较稳定
,则甲的射击成绩较稳定
C.“明天降雨的概率为![]() ”,表示明天有半天都在降雨
”,表示明天有半天都在降雨
D.了解一批电视机的使用寿命,适合用普查的方式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个坡角为30°的斜坡上有一电线杆AB,当太阳光与水平线成45°角时,测得该杆在斜坡上的影长BC为20m.求电线杆AB的高(精确到0.1m,参考数值:![]() ≈1.73,
≈1.73,![]() ≈1.41).
≈1.41).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A、B两点,与y轴交于点C,对称轴为直线x=﹣1,点B的坐标为(1,0),则下列结论:①AB=4;②b2﹣4ac>0;③ab<0;④a2﹣ab+ac<0,其中正确的结论有( )个.
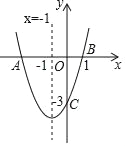
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国是世界上13个贫水国家之一.某校有800名在校学生,学校为鼓励学生节约用水,展开“珍惜水资源,节约每一滴水”系列教育活动.为响应学校号召,数学小组做了如下调查:
小亮为了解一个拧不紧的水龙头的滴水情况,记录了滴水时间和烧杯中的水面高度,如图1.小明设计了调查问卷,在学校随机抽取一部分学生进行了问卷调查,并制作出统计图.如图2和图3.
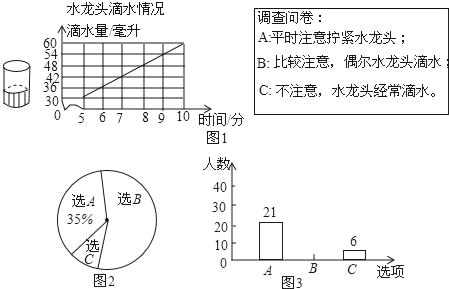
经结合图2和图3回答下列问题:
(1)参加问卷调查的学生人数为 人,其中选C的人数占调查人数的百分比为 .
(2)在这所学校中选“比较注意,偶尔水龙头滴水”的大概有 人.若在该校随机抽取一名学生,这名学生选B的概率为 .
请结合图1解答下列问题:
(3)在“水龙头滴水情况”图中,水龙头滴水量(毫升)与时间(分)可以用我们学过的哪种函数表示?请求出函数关系式.
(4)为了维持生命,每人每天需要约2400毫升水,该校选C的学生因没有拧紧水龙头,2小时浪费的水可维持多少人一天的生命需要?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC为4,面积为24,腰AC的垂直平分线EF分别交边AC,AB于点E,F,若D为BC边的中点,M为线段EF上一动点,则△CDM的周长的最小值为 ( )

A.8B.10C.12D.14
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com