
【题目】(1)解不等式组: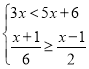 ;
;
(2)因式分解:(x﹣2)(x﹣8)+8;
(3)解方程:![]() +
+![]() =
=![]() ;
;
(4)解方程:(2x﹣1)2=3﹣6x.
【答案】(1)﹣3<x≤2;(2)(x﹣4)(x﹣6);(3) x=﹣5;(4)x=0.5或x=﹣1
【解析】
(1)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
(2)先去括号、合并同类项化简原式,再利用十字相乘法分解可得;
(3)根据解分式方程的步骤计算可得;
(4)利用因式分解法求解可得.
(1)解不等式3x<5x+6,得:x>﹣3,
解不等式![]() ,得:x≤2,
,得:x≤2,
则不等式组的解集为﹣3<x≤2;
(2)原式=x2﹣10x+24
=(x﹣4)(x﹣6);
(3)两边都乘以2(x﹣2),得:1+x﹣2=﹣6,
解得x=﹣5,
检验:x=﹣5时,2(x﹣2)≠0,
∴分式方程的解为x=﹣5;
(4)∵(2x﹣1)2+3(2x﹣1)=0,
∴(2x﹣1)(2x+2)=0,
则2x﹣1=0或2x+2=0,
解得x=0.5或x=﹣1.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD是等腰三角形,则PE的长为数___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,∠CAB的角平分线AD交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)若∠CAB=60°,DE=3![]() ,求AC的长.
,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
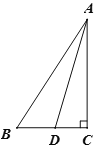
【题目】如图,Rt△ ABC中,∠ACB=90°,AD平分∠BAC, 作AD的垂直平分线EF交AD于点E,交BC的延长线于点F,交AB于点G,交AC于点H.
(1)依题意补全图形;
(2)求证:∠BAD=∠BFG;
(3)试猜想AB,FB和FD之间的数量关系并进行证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)阅读资料:
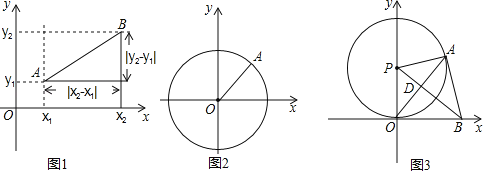
如图1,在平面之间坐标系xOy中,A,B两点的坐标分别为A(x1,y1),B(x2,y2),由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2,所以A,B两点间的距离为AB=![]() .
.
我们知道,圆可以看成到圆心距离等于半径的点的集合,如图2,在平面直角坐标系xoy中,A(x,y)为圆上任意一点,则A到原点的距离的平方为OA2=|x﹣0|2+|y﹣0|2,当⊙O的半径为r时,⊙O的方程可写为:x2+y2=r2.
问题拓展:如果圆心坐标为P(a,b),半径为r,那么⊙P的方程可以写为 .
综合应用:
如图3,⊙P与x轴相切于原点O,P点坐标为(0,6),A是⊙P上一点,连接OA,使tan∠POA=![]() ,作PD⊥OA,垂足为D,延长PD交x轴于点B,连接AB.
,作PD⊥OA,垂足为D,延长PD交x轴于点B,连接AB.
①证明AB是⊙P的切点;
②是否存在到四点O,P,A,B距离都相等的点Q?若存在,求Q点坐标,并写出以Q为圆心,以OQ为半径的⊙O的方程;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区规定学生每天户外体育活动时间不少于1小时.为了解学生参加户外体育活动的情况,对部分学生每天参加户外体育活动的时间进行了随机抽样调查,并将调查结果绘制成如下的统计表(不完整).
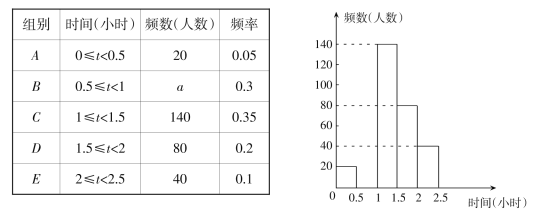
请根据图表中的信息,解答下列问题:
(1)写出表中a的值,将频数分布直方图补全;
(2)该区8000名学生中,每天户外体育活动的时间不足1小时的学生大约有多少名?
(3)若从参加户外体育活动时间最长的3名男生和1名女生中随机抽取两名,请用画树状图或列表法求恰好抽到1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
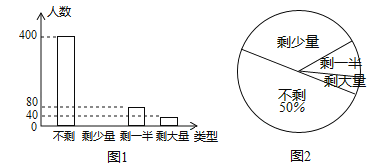
【题目】某企业工会开展“一周工作量完成情况”调查活动,随机调查了部分员工一周的工作量剩余情况,并将调查结果统计后绘制成如图 1 和图 2 所示的不完整统计图 .
(1) 被调查员工的人数为 人:
(2) 把条形统计图补充完整;
(3) 若该企业有员工 10000 人,请估计该企业某周的工作量完成情况为“剩少量”的员工有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
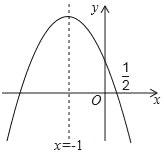
【题目】如图,抛物线y=ax2+bx+c的对称轴是x=﹣1,且过点(![]() ,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a+4c=10b;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有错误的结论有( )个.
,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a+4c=10b;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有错误的结论有( )个.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com