
【题目】如图,Rt△ ABC中,∠ACB=90°,AD平分∠BAC, 作AD的垂直平分线EF交AD于点E,交BC的延长线于点F,交AB于点G,交AC于点H.
(1)依题意补全图形;
(2)求证:∠BAD=∠BFG;
(3)试猜想AB,FB和FD之间的数量关系并进行证明.
【答案】(1)补图见解析;(2)证明见解析;(3)![]() ,证明见解析.
,证明见解析.
【解析】
(1)根据题意补全图形;
(2)根据角平分线的定义得到∠BAD=∠CAD.在Rt△AEH和Rt△CFH中,根据三角形内角和定理得到∠CFH=∠CAD,等量代换即可得到结论;
(3)由线段垂直平分线的性质得到AF=FD,通过证明∠BAF=90°.在Rt△BAF中,利用勾股定理即可得到结论.
(1)补全图形如图;
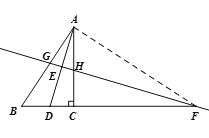
(2)∵AD平分∠BAC,∴∠BAD=∠CAD.
∵FE⊥AD,∠ACF=90°,∠AHE=∠CHF,∴∠CFH=∠CAD,∴∠BAD=∠CFH,即∠BAD=∠BFG.
(3)猜想:![]() .证明如下:
.证明如下:
连接AF.
∵EF为AD的垂直平分线,∴AF=FD,∠DAF=∠ADF,∴∠DAC+∠CAF=∠B+∠BAD.
∵AD是角平分线,∴∠BAD=∠CAD,∴∠CAF=∠ B,∴∠BAF=∠BAC+∠CAF=∠BAC+∠B=90°,∴![]() ,∴
,∴![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE="10," 求直角梯形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣![]() x2+bx+c经过点(1,0),(0,
x2+bx+c经过点(1,0),(0,![]() ).
).
(1)求该抛物线的函数表达式;
(2)将抛物线y=﹣![]() x2+bx+c平移,使其顶点恰好落在原点,请写出一种平移的方法及平移后的函数表达式.
x2+bx+c平移,使其顶点恰好落在原点,请写出一种平移的方法及平移后的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(发现问题)爱好数学的小明在做作业时碰到这样的一道题目:
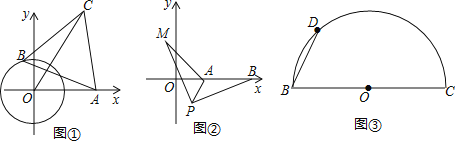
如图①,点O为坐标原点,⊙O的半径为1,点A(2,0).动点B在⊙O上,连结AB,作等边△ABC(A,B,C为顺时针顺序),求OC的最大值
(解决问题)小明经过多次的尝试与探索,终于得到解题思路:在图①中,连接OB,以OB为边在OB的左侧作等边三角形BOE,连接AE.
(1)请你找出图中与OC相等的线段,并说明理由;
(2)求线段OC的最大值.
(灵活运用)
(3)如图②,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,求线段AM长的最大值及此时点P的坐标.
(迁移拓展)
(4)如图③,BC=4![]() ,点D是以BC为直径的半圆上不同于B、C的一个动点,以BD为边作等边△ABD,请直接写出AC的最值.
,点D是以BC为直径的半圆上不同于B、C的一个动点,以BD为边作等边△ABD,请直接写出AC的最值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCO中,O(0,0),C(0,3),A(a,0),(a≥3),以A为旋转中心顺时针旋转矩形ABCO得到矩形AFED.
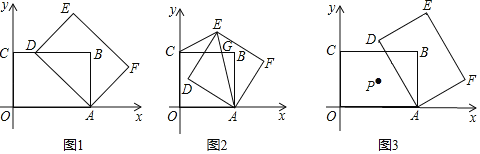
(1)如图1,当点D落在边BC上时,求BD的长(用a的式子表示);
(2)如图2,当a=3时,矩形AFED的对角线AE交矩形ABCO的边BC于点G,连结CE,若△CGE是等腰三角形,求直线BE的解析式;
(3)如图3,矩形ABCO的对称中心为点P,当P,B关于AD对称时,求出a的值,此时在x轴、y轴上是否分别存在M,N使得四边形EFMN为平行四边形,若存在直接写出M,N坐标,不存在说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】动画片《小猪佩奇》分靡全球,受到孩子们的喜爱.现有4张《小猪佩奇》角色卡片,分别是A佩奇,B乔治,C佩奇妈妈,D佩奇爸爸(四张卡片除字母和内容外,其余完全相同).姐弟两人做游戏,他们将这四张卡片混在一起,背面朝上放好.
(1)姐姐从中随机抽取一张卡片,恰好抽到A佩奇的概率为 ;
(2)若两人分别随机抽取一张卡片(不放回),请用列表或画树状图的分方法求出恰好姐姐抽到A佩奇弟弟抽到B乔治的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b2﹣4ax>0;②2a+b>0;③abc<0;④4a﹣2b+c<0;⑤a+b+c>0.其中正确的个数是( )
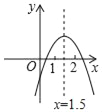
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
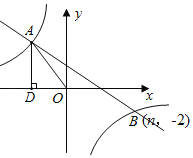
【题目】如图所示,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象交于第二、四象限A、B两点,过点A作AD⊥x轴于D,AD=4,sin∠AOD=
(m≠0)的图象交于第二、四象限A、B两点,过点A作AD⊥x轴于D,AD=4,sin∠AOD=![]() ,且点B的坐标为(n,-2).
,且点B的坐标为(n,-2).
(1)求一次函数与反比例函数的解析式;
(2)E是y轴上一点,且△AOE是等腰三角形,请直接写出所有符合条件的E点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com