
【题目】矩形ABCO中,O(0,0),C(0,3),A(a,0),(a≥3),以A为旋转中心顺时针旋转矩形ABCO得到矩形AFED.
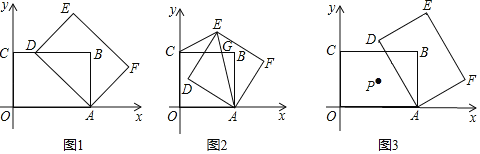
(1)如图1,当点D落在边BC上时,求BD的长(用a的式子表示);
(2)如图2,当a=3时,矩形AFED的对角线AE交矩形ABCO的边BC于点G,连结CE,若△CGE是等腰三角形,求直线BE的解析式;
(3)如图3,矩形ABCO的对称中心为点P,当P,B关于AD对称时,求出a的值,此时在x轴、y轴上是否分别存在M,N使得四边形EFMN为平行四边形,若存在直接写出M,N坐标,不存在说明理由.
【答案】(1)BD=![]() ;(2)y=﹣x+6;(3)M(
;(2)y=﹣x+6;(3)M(![]() ,0),N(0,
,0),N(0,![]() )
)
【解析】
(1)如图1,当点D落在边BC上时,BD2=AD2-AB2,即可求解;
(2)分CG=EG、CE=GE、CE=CG三种情况分别求解;
(3)①由点P为矩形ABCO的对称中心,得到![]() 求得直线PB的解析式为
求得直线PB的解析式为![]() ,得到直线AD的解析式为:
,得到直线AD的解析式为:![]() ,解方程即可得到结论;②根据①中的结论得到直线AD 的解析式为
,解方程即可得到结论;②根据①中的结论得到直线AD 的解析式为![]() ,求得∠DAB=30°,连接AE,推出A,B,E三点共线,求得
,求得∠DAB=30°,连接AE,推出A,B,E三点共线,求得![]() ,设M(m,0),N(0,n),解方程组即可得到结论.
,设M(m,0),N(0,n),解方程组即可得到结论.
(1)如图1,
在矩形ABCO中,∠B=90°
当点D落在边BC上时,BD2=AD2﹣AB2,
∵C(0,3),A(a,0)
∴AB=OC=3,AD=AO=a,
∴BD=![]() ;
;
(2)如图2,连结AC,
∵a=3,∴OA=OC=3,
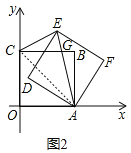
∴矩形ABCO是正方形,∴∠BCA=45°,
设∠ECG的度数为x,
∴AE=AC,∴∠AEC=∠ACE=45°+x,
①当CG=EG时,x=45°+x,
解得x=0,不合题意,舍去;
②当CE=GE时,如图2,
∠ECG=∠EGC=x
∵∠ECG+∠EGC+∠CEG=180°,
∴x+x+(45°+x)=180°,解得x=45°,
∴∠AEC=∠ACE=90°,不合题意,舍去;
③当CE=CG时,∠CEG=∠CGE=45°+x,
∵∠ECG+∠EGC+∠CEG=180°,
∴x+(45°+x)+(45°+x)=180°,解得x=30°,
∴∠AEC=∠ACE=75°,∠CAE=30°
如图3,连结OB,交AC于点Q,过E作EH⊥AC于H,连结BE,
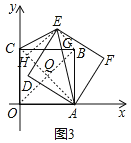
∴EH=![]() AE=
AE=![]() AC,BQ=
AC,BQ=![]() AC,
AC,
∴EH=BQ,EH∥BQ且∠EHQ=90°
∴四边形EHQB是矩形
∴BE∥AC,
设直线BE的解析式为y=﹣x+b,
∵点B(3,3)在直线上,则b=6,
∴直线BE的解析式为y=﹣x+6;
(3)①∵点P为矩形ABCO的对称中心,
∴![]() ,
,
∵B(a,3),
∴PB的中点坐标为:![]() ,
,
∴直线PB的解析式为![]() ,
,
∵当P,B关于AD对称,
∴AD⊥PB,
∴直线AD的解析式为:![]() ,
,
∵直线AD过点![]() ,∴
,∴![]() ,
,
解得:a=±3![]() ,
,
∵a≥3,
∴a=3![]() ;
;
②存在M,N;
理由:∵a=3![]() ,
,
∴直线AD 的解析式为y=﹣![]() x+9,
x+9,
∴∴∠DAO=60°,
∴∠DAB=30°,
连接AE,
∵AD=OA=3![]() ,DE=OC=3,
,DE=OC=3,
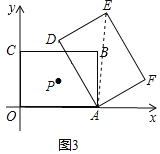
∴∠EAD=30°,
∴A,B,E三点共线,
∴AE=2DE=6,
∴![]() ,
,
设M(m,0),N(0,n),
∵四边形EFMN是平行四边形,
∴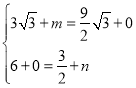 ,
,
解得: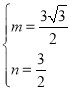 ,
,
∴M(![]() ,0),N(0,
,0),N(0,![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 且垂直于
且垂直于![]() 的直线
的直线![]() 交
交![]() 轴于点
轴于点![]() ,点
,点![]() 是
是![]() 轴下方抛物线上的一个动点,过点
轴下方抛物线上的一个动点,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,交直线
,交直线![]() 于点
于点![]() .
.
(1)求抛物线的解析式;
(2)设点![]() 的横坐标为
的横坐标为![]() ,当
,当![]() 时,求
时,求![]() 的值;
的值;
(3)当直线![]() 为抛物线的对称轴时,以点
为抛物线的对称轴时,以点![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() ,点
,点![]() 为
为![]() 上的一个动点,求
上的一个动点,求![]() 的最小值.
的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BE平分∠ABC交AC于点E,过点E作ED∥BC交AB于点D.
(1)求证:AEBC=BDAC;
(2)如果S△ADE=3,S△BDE=2,DE=6,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,∠CAB的角平分线AD交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)若∠CAB=60°,DE=3![]() ,求AC的长.
,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
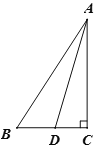
【题目】如图,Rt△ ABC中,∠ACB=90°,AD平分∠BAC, 作AD的垂直平分线EF交AD于点E,交BC的延长线于点F,交AB于点G,交AC于点H.
(1)依题意补全图形;
(2)求证:∠BAD=∠BFG;
(3)试猜想AB,FB和FD之间的数量关系并进行证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)阅读资料:
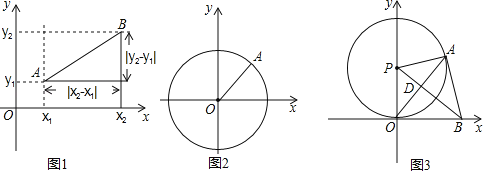
如图1,在平面之间坐标系xOy中,A,B两点的坐标分别为A(x1,y1),B(x2,y2),由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2,所以A,B两点间的距离为AB=![]() .
.
我们知道,圆可以看成到圆心距离等于半径的点的集合,如图2,在平面直角坐标系xoy中,A(x,y)为圆上任意一点,则A到原点的距离的平方为OA2=|x﹣0|2+|y﹣0|2,当⊙O的半径为r时,⊙O的方程可写为:x2+y2=r2.
问题拓展:如果圆心坐标为P(a,b),半径为r,那么⊙P的方程可以写为 .
综合应用:
如图3,⊙P与x轴相切于原点O,P点坐标为(0,6),A是⊙P上一点,连接OA,使tan∠POA=![]() ,作PD⊥OA,垂足为D,延长PD交x轴于点B,连接AB.
,作PD⊥OA,垂足为D,延长PD交x轴于点B,连接AB.
①证明AB是⊙P的切点;
②是否存在到四点O,P,A,B距离都相等的点Q?若存在,求Q点坐标,并写出以Q为圆心,以OQ为半径的⊙O的方程;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
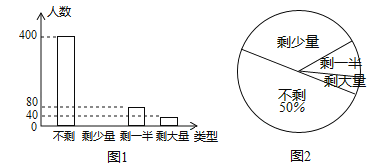
【题目】某企业工会开展“一周工作量完成情况”调查活动,随机调查了部分员工一周的工作量剩余情况,并将调查结果统计后绘制成如图 1 和图 2 所示的不完整统计图 .
(1) 被调查员工的人数为 人:
(2) 把条形统计图补充完整;
(3) 若该企业有员工 10000 人,请估计该企业某周的工作量完成情况为“剩少量”的员工有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ ABC中,∠ACB=90°,AD平分∠BAC, 作AD的垂直平分线EF交AD于点E,交BC的延长线于点F,交AB于点G,交AC于点H.
(1)依题意补全图形;
(2)求证:∠BAD=∠BFG;
(3)试猜想AB,FB和FD之间的数量关系并进行证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com