
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 且垂直于
且垂直于![]() 的直线
的直线![]() 交
交![]() 轴于点
轴于点![]() ,点
,点![]() 是
是![]() 轴下方抛物线上的一个动点,过点
轴下方抛物线上的一个动点,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,交直线
,交直线![]() 于点
于点![]() .
.
(1)求抛物线的解析式;
(2)设点![]() 的横坐标为
的横坐标为![]() ,当
,当![]() 时,求
时,求![]() 的值;
的值;
(3)当直线![]() 为抛物线的对称轴时,以点
为抛物线的对称轴时,以点![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() ,点
,点![]() 为
为![]() 上的一个动点,求
上的一个动点,求![]() 的最小值.
的最小值.

【答案】(1)y![]() x2
x2![]() x﹣3;(2)
x﹣3;(2)![]() ;(3)
;(3)![]() .
.
【解析】
对于(1),结合已知先求出点B和点C的坐标,再利用待定系数法求解即可;
对于(2),在Rt△OAC中,利用三角函数的知识求出∠OAC的度数,再利用角平分线的定义求出∠OAD的度数,进而得到点D的坐标;接下来求出直线AD的解析式,表示出点P,H,F的坐标,再利用两点间的距离公式可完成解答;对于(3),首先求出⊙H的半径,在HA上取一点K,使得HK=14,此时K(-![]() ,
,![]() );然后由HQ2=HK·HA,得到△QHK∽△AHQ,再利用相似三角形的性质求出KQ=
);然后由HQ2=HK·HA,得到△QHK∽△AHQ,再利用相似三角形的性质求出KQ=![]() AQ,进而可得当E、Q、K共线时,
AQ,进而可得当E、Q、K共线时,![]() AQ+EQ的值最小,据此解答.
AQ+EQ的值最小,据此解答.
(1)由题意A(![]() ,0),B(﹣3
,0),B(﹣3![]() ,0),C(0,﹣3),设抛物线的解析式为y=a(x+3
,0),C(0,﹣3),设抛物线的解析式为y=a(x+3![]() )(x
)(x![]() ),把C(0,﹣3)代入得到a
),把C(0,﹣3)代入得到a![]() ,∴抛物线的解析式为y
,∴抛物线的解析式为y![]() x2
x2![]() x﹣3.
x﹣3.
(2)在Rt△AOC中,tan∠OAC![]() ,∴∠OAC=60°.
,∴∠OAC=60°.
∵AD平分∠OAC,∴∠OAD=30°,∴OD=OAtan30°=1,∴D(0,﹣1),∴直线AD的解析式为y![]() x﹣1,由题意P(m,
x﹣1,由题意P(m,![]() m2
m2![]() m﹣3),H(m,
m﹣3),H(m,![]() m﹣1),F(m,0).
m﹣1),F(m,0).
∵FH=PH,∴1![]() m﹣1﹣(
m﹣1﹣(![]() m2
m2![]() m﹣3)
m﹣3)
解得m![]() 或
或![]() (舍弃),∴当FH=HP时,m的值为
(舍弃),∴当FH=HP时,m的值为![]() .
.
(3)如图,∵PF是对称轴,∴F(![]() ,0),H(
,0),H(![]() ,﹣2).
,﹣2).
∵AH⊥AE,∴∠EAO=60°,∴EO![]() OA=3,∴E(0,3).
OA=3,∴E(0,3).
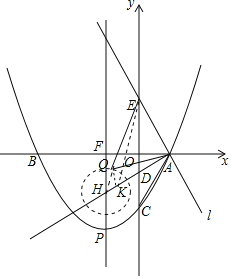
∵C(0,﹣3),∴HC![]() 2,AH=2FH=4,∴QH
2,AH=2FH=4,∴QH![]() CH=1,在HA上取一点K,使得HK
CH=1,在HA上取一点K,使得HK![]() ,此时K(
,此时K(![]() ).
).
∵HQ2=1,HKHA=1,∴HQ2=HKHA,∴![]() .
.
∵∠QHK=∠AHQ,∴△QHK∽△AHQ,∴![]() ,∴KQ
,∴KQ![]() AQ,∴
AQ,∴![]() AQ+QE=KQ+EQ,∴当E、Q、K共线时,
AQ+QE=KQ+EQ,∴当E、Q、K共线时,![]() AQ+QE的值最小,最小值
AQ+QE的值最小,最小值![]() .
.


 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
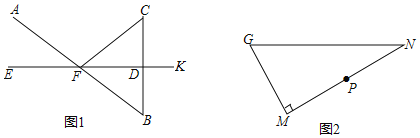
【题目】(1)如图1,已知EK垂直平分BC,垂足为D,AB与EK相交于点F,连接CF.求证:∠AFE=∠CFD.
(2)如图2,在Rt△GMN中,∠M=90°,P为MN的中点.
①用直尺和圆规在GN边上求作点Q,使得∠GQM=∠PQN(保留作图痕迹,不要求写作法);
②在①的条件下,如果∠G=60°,那么Q是GN的中点吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,O是AC、BD的交点,过点O 与AC垂直的直线交边AD于点E,若□ABCD的周长为22cm,则△CDE的周长为( ).

A. 8cm B. 10cm C. 11cm D. 12cm
查看答案和解析>>
科目:初中数学 来源: 题型:
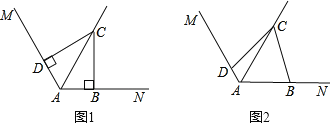
【题目】已知∠MAN=120°,AC平分∠MAN,点B、D分别在AN、AM上.
(1)如图1,若∠ABC=∠ADC=90°,请你探索线段AD、AB、AC之间的数量关系,并证明之;
(2)如图2,若∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE="10," 求直角梯形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
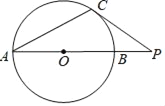
【题目】如图,C是⊙O上一点,点P在直径AB的延长线上,⊙O的半径为3,PB=2,PC=4.
(1)求证:PC是⊙O的切线.
(2)求tan∠CAB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC的底边BC=20,面积为120,点F在边BC上,且BF=3FC,EG是腰AC的垂直平分线,若点D在EG上运动,则△CDF周长的最小值为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCO中,O(0,0),C(0,3),A(a,0),(a≥3),以A为旋转中心顺时针旋转矩形ABCO得到矩形AFED.
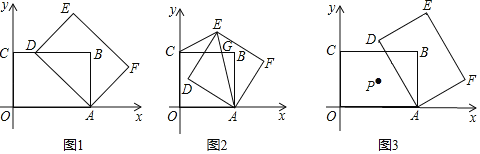
(1)如图1,当点D落在边BC上时,求BD的长(用a的式子表示);
(2)如图2,当a=3时,矩形AFED的对角线AE交矩形ABCO的边BC于点G,连结CE,若△CGE是等腰三角形,求直线BE的解析式;
(3)如图3,矩形ABCO的对称中心为点P,当P,B关于AD对称时,求出a的值,此时在x轴、y轴上是否分别存在M,N使得四边形EFMN为平行四边形,若存在直接写出M,N坐标,不存在说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com