
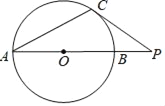
【题目】如图,C是⊙O上一点,点P在直径AB的延长线上,⊙O的半径为3,PB=2,PC=4.
(1)求证:PC是⊙O的切线.
(2)求tan∠CAB的值.
【答案】(1)见解析;(2)tan∠CAB=![]() .
.
【解析】
(1)可以证明OC2+PC2=OP2得△OCP是直角三角形,即OC⊥PC,PC是⊙O的切线;
(2)AB是直径,得∠ACB=90°,通过角的关系可以证明△PBC∽△PCA,进而![]() ,得出tan∠ACB=
,得出tan∠ACB=![]() .
.
(1)如图,连接OC、BC,
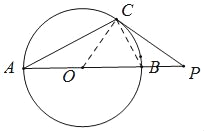
∵⊙O的半径为3,PB=2,
∴OC=OB=3,OP=OB+PB=5,
∵PC=4,
∴OC2+PC2=OP2,
∴△OCP是直角三角形,
∴OC⊥PC,
∴PC是⊙O的切线.
(2)∵AB是直径,
∴∠ACB=90°,
∴∠ACO+∠OCB=90°.
∵OC⊥PC,
∴∠BCP+∠OCB=90°,
∴∠BCP=∠ACO.
∵OA=OC,
∴∠A=∠ACO,
∴∠A=∠BCP.
在△PBC和△PCA中:
∠BCP=∠A,∠P=∠P,
∴△PBC∽△PCA,
∴![]() =
=![]() =
=![]() =
=![]()
∴tan∠CAB=![]() =
=![]()


科目:初中数学 来源: 题型:
【题目】已知△ABC为等边三角形,P是直线AC上一点,AD⊥BP于D,以AD为边作等边△ADE(D,E在直线AC异侧).
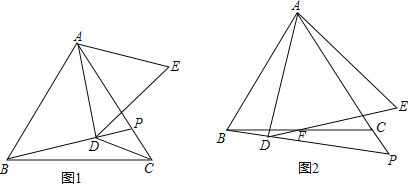
(1)如图1,若点P在边AC上,连CD,且∠BDC=150°,则![]() = ;(直接写结果)
= ;(直接写结果)
(2)如图2,若点P在AC延长线上,DE交BC于F求证:BF=CF;
(3)在图2中,若∠PBC=15°,AB=![]() ,请直接写出CP的长 .
,请直接写出CP的长 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄河,既是一条源远流长、波澜壮阔的自然河,又是一条孕育中华民族灿烂文明的母亲河.数学课外实践活动中,小林和同学们在黄河南岸小路上的A,B两点处,用测角仪分别对北岸的观景亭D进行测量.如图,测得∠DAC=45°,∠DBC=65°.若AB=200米,求观景亭D到小路AC的距离约为多少米?(结果精确到1米,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 且垂直于
且垂直于![]() 的直线
的直线![]() 交
交![]() 轴于点
轴于点![]() ,点
,点![]() 是
是![]() 轴下方抛物线上的一个动点,过点
轴下方抛物线上的一个动点,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,交直线
,交直线![]() 于点
于点![]() .
.
(1)求抛物线的解析式;
(2)设点![]() 的横坐标为
的横坐标为![]() ,当
,当![]() 时,求
时,求![]() 的值;
的值;
(3)当直线![]() 为抛物线的对称轴时,以点
为抛物线的对称轴时,以点![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() ,点
,点![]() 为
为![]() 上的一个动点,求
上的一个动点,求![]() 的最小值.
的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】广安市某楼盘准备以每平方米6000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4860元的均价开盘销售.
(1)求平均每次下调的百分率.
(2)某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,一次性送装修费每平方米80元,试问哪种方案更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD是等腰三角形,则PE的长为数___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BE平分∠ABC交AC于点E,过点E作ED∥BC交AB于点D.
(1)求证:AEBC=BDAC;
(2)如果S△ADE=3,S△BDE=2,DE=6,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)阅读资料:
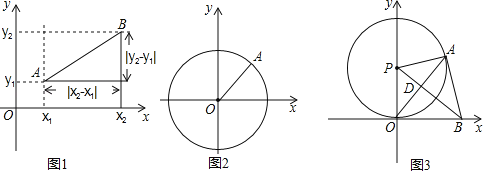
如图1,在平面之间坐标系xOy中,A,B两点的坐标分别为A(x1,y1),B(x2,y2),由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2,所以A,B两点间的距离为AB=![]() .
.
我们知道,圆可以看成到圆心距离等于半径的点的集合,如图2,在平面直角坐标系xoy中,A(x,y)为圆上任意一点,则A到原点的距离的平方为OA2=|x﹣0|2+|y﹣0|2,当⊙O的半径为r时,⊙O的方程可写为:x2+y2=r2.
问题拓展:如果圆心坐标为P(a,b),半径为r,那么⊙P的方程可以写为 .
综合应用:
如图3,⊙P与x轴相切于原点O,P点坐标为(0,6),A是⊙P上一点,连接OA,使tan∠POA=![]() ,作PD⊥OA,垂足为D,延长PD交x轴于点B,连接AB.
,作PD⊥OA,垂足为D,延长PD交x轴于点B,连接AB.
①证明AB是⊙P的切点;
②是否存在到四点O,P,A,B距离都相等的点Q?若存在,求Q点坐标,并写出以Q为圆心,以OQ为半径的⊙O的方程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com