
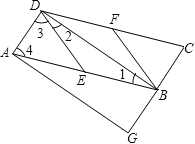
【题目】已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.

(1)求证:△ADE≌△CBF;
(2)若四边形 BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
【答案】(1)证明:∵四边形ABCD是平行四边形,
∴∠4=∠C,AD=CB,AB=CD.
∵点E、F分别是AB、CD的中点,
∴AE=![]() AB,CF=
AB,CF=![]() CD.
CD.
∴AE=CF.
∴△ADE≌△CBF(SAS).
(2)解:当四边形BEDF是菱形时,四边形AGBD是矩形.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∵AG∥BD,
∴四边形AGBD是平行四边形.
∵四边形BEDF是菱形,
∴DE=BE.
∵AE=BE,
∴AE=BE=DE.
∴∠1=∠2,∠3=∠4.
∵∠1+∠2+∠3+∠4=180°,
∴2∠2+2∠3=180°.
∴∠2+∠3=90°.
即∠ADB=90°.
∴四边形AGBD是矩形.
【解析】试题分析:本题主要考查了平行四边形的基本性质和矩形的判定及全等三角形的判定.平行四边形基本性质:①平行四边形两组对边分别平行;②平行四边形的两组对边分别相等;③平行四边形的两组对角分别相等;④平行四边形的对角线互相平分.三角形全等的判定条件:SSS,SAS,AAS,ASA.
(1)在证明全等时常根据已知条件,分析还缺什么条件,然后用(SAS,ASA,SSS)来证明全等; (2)先由菱形的性质得出AE=BE=DE,再通过角之间的关系求出∠2+∠3=90°即∠ADB=90°,所以判定四边形AGBD是矩形.
试题解析:(1)∵四边形ABCD是平行四边形,
∴∠4=∠C,AD=CB,AB=CD.
∵点E、F分别是AB、CD的中点,
∴AE=![]() AB,CF=
AB,CF=![]() CD.
CD.
∴AE=CF.
在△AED和△CBF中,
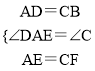 ,
,
∴△ADE≌△CBF(SAS).
(2)当四边形BEDF是菱形时,四边形AGBD是矩形.
∵四边形ABCD是平行四边形,
∴AD∥BC.
∵AG∥BD,
∴四边形AGBD是平行四边形.
∵四边形BEDF是菱形,
∴DE=BE.
∵AE=BE,
∴AE=BE=DE.
∴∠1=∠2,∠3=∠4.
∵∠1+∠2+∠3+∠4=180°,
∴2∠2+2∠3=180°.
∴∠2+∠3=90°.
即∠ADB=90°.
∴四边形AGBD是矩形.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做等邻边四边形。.
(1)概念理解
如图1,在四边形ABCD中,添加一个条件使得四边形ABCD是等邻边四边形。请写出你添加的一个条件;
(2)问题探究
小明猜想:对角线互相平分的等邻边四边形是菱形.她的猜想正确吗?请说明理由.
如图2,小明面了一个Rt△ABC,其中∠ABC=90°,AB=2,BC=1,井将Rt△ABC沿∠ABC的平分线BB′方向平移得到△A′B′C′,连结AA′,BC′.小明要是平移后的四边形ABC′A′是“等邻边四边形”应平移多少距离(即线段BB′的长)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次“献爱心手拉手”捐款活动中,某数学兴趣小组对学校所在社区部分捐款户数进行调查和分组统计,将数据整理成以下统计表和统计图(信息不完整),已知A,B两组捐款户数的比为1∶5.
捐款户数分组统计表
组别 | 捐款数(x)元 | 户数 |
A | 1≤x<100 | a |
B | 100≤x<200 | 10 |
C | 200≤x<300 | 20 |
D | 300≤x<400 | 14 |
E | x≥400 | 4 |
请结合以上信息解答下列问题:
(1)a=____________,本次调查的样本容量是____________;
(2)补全捐款户数统计表和统计图;
(3)若该社区有600户居民,根据以上信息估计全社区捐款不少于300元的户数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条直线上依次有A、B、C三个港口,A、B两港相距30千米,B、C两港相距90千米.甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终达到C港.甲0.5小时到达B港,此时两船相距15千米.
求:(1)甲船何时追上乙,此时乙离C港多远?
(2)何时甲乙两船相距10千米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com